NP 问题
定义: 非确定型图灵机在多项式时间内可以找到解的问题,简单说就是可以在多项式时间里验证一个解的问题。
延伸: $\text{P}$ 问题属于 $\text{NP}$ 问题,但 $\text{P}$ 问题是否等于 $\text{NP}$ 问题,目前仍然是一个世界难题。所以请注意 $\text{NP}$ 问题绝不是指在多项式时间内找不到解的问题,切勿混淆概念。
P 问题
定义: 确定型图灵机在多项式时间内可以解决的问题,简单说就是可以在多项式时间里解决的问题。
延伸: 通常来说,$\text{P}$ 问题在生活中更有意义。因为可以在多项式时间里解决就意味着问题复杂度不会随着数据规模的扩大而指数爆炸,在生活中更容易被解决。
补充一句,所有的 $\text{P}$ 问题都是 $\text{NP}$ 问题。
约化(Reducibility)
要引出 $\text{NPC}$ 问题,就必须提到约化。
定义: $\text{A}$ 问题可以约化成 $\text{B}$ 问题,代表可以用 $\text{B}$ 问题的解法解决 $\text{A}$ 问题。
举例: “求解一元一次方程” 问题可以约化成 “求解一元二次方程” 问题,只需要令 “求解一元二次方程” 问题中二次项系数为 $0$ 即可解决 “求解一元一次方程” 问题。
因此可以发现,约化的过程是难度升级的过程。问题 $\text{A}$ 可约化成问题 $\text{B}$,代表 $\text{B}$ 问题的时间复杂度高于或者等于 $\text{A}$ 问题的时间复杂度,即 $\text{A}$ 问题不比 $\text{B}$ 问题难。因此一个问题约化成另一个问题,时间复杂度增加了,问题的应用范围也扩大了。
继续思考还可以发现约化具有传递性。如果 $\text{A}$ 问题可以约化成 $\text{B}$ 问题,$\text{B}$ 问题可以约化成 $\text{C}$ 问题,则 $\text{A}$ 问题一定可以约化成 $\text{C}$ 问题。而且如果 $\text{C}$ 问题可以解决,那么 $\text{A}$、$\text{B}$ 问题均可被解决。
NPC 问题
$\text{NPC}$ 问题即 $\text{NP-complete}$ 问题、$\text{NP}$ 完全问题。
定义: $\text{NPC}$ 问题即为所有 $\text{NP}$ 问题可以约化到的一个问题,是所有 $\text{NP}$ 问题中最复杂的问题。
NPC 问题满足条件:
-
该问题是一个 $\text{NP}$ 问题。
-
该问题可以由一个已知的 $\text{NPC}$ 问题约化到它。
第一个 NPC 问题: 第一个 $\text{NPC}$ 问题是逻辑电路问题,即 “给定一个逻辑电路,是否存在一种输入使输出为 $\text{True}$”。
该问题属于 $\text{NPC}$ 问题的证明十分复杂,如果感兴趣可以自行查阅相关资料。引用一篇文章中对于其证明过程的大致表述,本文的内容也主要参考该篇文章。
逻辑电路问题属于 $\text{NPC}$ 问题的证明过程相当复杂,其大概意思是说任意一个 $\text{NP}$ 问题的输入和输出都可以转换成逻辑电路的输入和输出(想想计算机内部也不过是一些 $0$ 和 $1$ 的运算),因此对于一个 $\text{NP}$ 问题来说,问题转化为了求出满足结果为 $\text{True}$ 的一个输入(即一个可行解)。
常见的旅行商问题、$\text{Hamilton}$ 回路问题也都属于 $\text{NPC}$ 问题。
NP-hard 问题
$\text{NP-hard}$ 问题即满足 $\text{NPC}$ 问题的第二个条件但不一定满足第一个条件,即所有 $\text{NP}$ 问题都能在多项式时间约化到它,因此 $\text{NP-hard}$ 问题要比 $\text{NPC}$ 问题范围广,$\text{NP-hard}$ 问题不一定是 $\text{NP}$ 问题。
即使 $\text{NPC}$ 问题发现了多项式时间内的算法,$\text{NP-hard}$ 问题可能仍然无法在多项式时间内解决,甚至 $\text{NP-hard}$ 问题有可能比所有的 $\text{NPC}$ 问题的时间复杂度更高且更难解决。
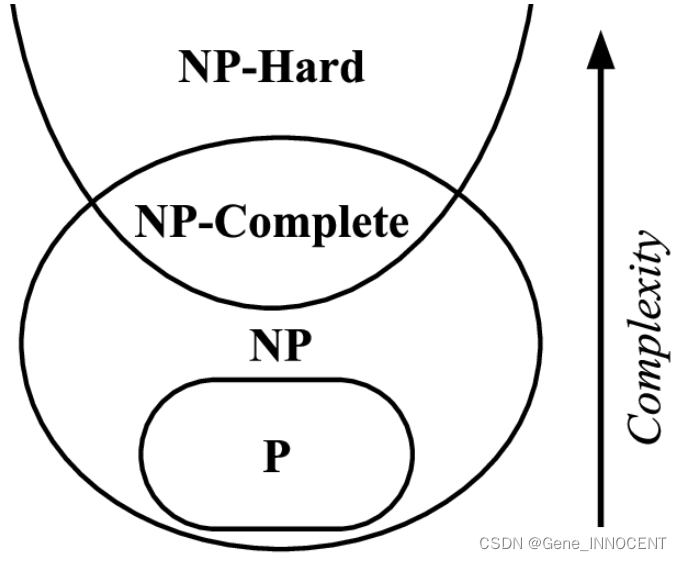
上述四类问题的关系如下图所示:
后记
本文只能算是简单的介绍了一些 $\text{NP}$、$\text{P}$、$\text{NPC}$、$\text{NP-hard}$ 这几个概念,感兴趣的读者可以继续查阅相关知识体会该 $\text{P=NP}?$ 这一世界难题的魅力。
愿 $\text{P=NP}?$ 早日得以解决,我们可以早日攀登上这计算机科学的顶峰。💪💪💪