本文主要针对线性代数中的正定矩阵、实对称矩阵、矩阵特征值分解以及矩阵 SVD 分解进行总结。
正定矩阵
1. 概念
首先正定矩阵是定义在对称矩阵的基础上,其次对于任意非零向量 $\textbf{x}$,若 $\textbf{x}^T\boldsymbol{A}\textbf{x}>0$ 恒成立,则矩阵 $\boldsymbol{A}$ 为正定矩阵;若$\textbf{x}^T\boldsymbol{A}\textbf{x}\geq 0$ 恒成立,则矩阵 $\boldsymbol{A}$ 为半正定矩阵。
2. 物理意义
任意非零向量 $\textbf{x}$ 经过矩阵 $\boldsymbol{A}$ 线性变换后,与原先向量的夹角 $\leq 90$ 度。
3. 其他充要条件
-
充要条件1: 矩阵 $\boldsymbol{A}$ 的全部特征值都是正数
-
推论:若 $\boldsymbol{A}$ 正定,则 $|\boldsymbol{A}|>0$,即 $\boldsymbol{A}$ 可逆(有时会根据矩阵正定来判断是否可逆)
-
推论: 若 $\boldsymbol{A}$ 正定,则 $\boldsymbol{A}$ 与单位阵合同,即存在可逆阵 $\boldsymbol{C}$,使得 $\boldsymbol{C}^T\boldsymbol{A}\boldsymbol{C}=\boldsymbol{E}$ 成立
-
充要条件2:矩阵 $\boldsymbol{A}$ 的各阶顺序主子式都是正数,即 $\Delta_i>0$
-
其中 $\Delta_i$ 表示矩阵 $\boldsymbol{A}$ 前 $i$ 行与前 $i$ 列组成的子矩阵的行列式的值
-
推论:$|\boldsymbol{A}|>0$ 则 $\boldsymbol{A}$ 一定可逆
实对称矩阵
1. 概念
矩阵为方阵,其中元素均为实数,且 $\boldsymbol{A}=\boldsymbol{A}^T$。
2. 性质
性质1:实对称矩阵的特征值都是实数。- 假设 $\lambda$、$\textbf{x}$ 分别为矩阵 $\boldsymbol{A}$ 的特征值、特征向量,即 $\boldsymbol{A}\textbf{x}=\lambda \textbf{x}$
- 等式两边取共轭,即 $\overline{a+bi}=a-bi$,$\overline{\boldsymbol{A}}\overline{\textbf{x}}=\overline{\lambda} \overline{\textbf{x}}$,$\boldsymbol{A}$ 是实对称矩阵,因此 $\boldsymbol{A}=\boldsymbol{A}^T=\overline{\boldsymbol{A}}$,即 $\boldsymbol{A}\overline{\textbf{x}}=\overline{\lambda} \overline{\textbf{x}}$
- 等式两边取转置,则 $\textbf{x}^T\boldsymbol{A}=\lambda \textbf{x}^T$
- $\textbf{x}^T\boldsymbol{A}\overline{x}=\overline{\lambda}\textbf{x}^T\overline{\textbf{x}}=\lambda \textbf{x}^T\overline{\textbf{x}}$
- $(\lambda-\overline{\lambda})\left|\textbf{x}\right|_2^2=0$,由于 $\left|\textbf{x}\right|_2^2>0$,因此 $\lambda=\overline{\lambda}$,$\lambda$ 为实数
性质2:实对称矩阵不同特征值所对应的特征向量必定正交。- 假设 $\boldsymbol{A}\textbf{x}_1=\lambda_1 \textbf{x}_1$ 与 $\boldsymbol{A}\textbf{x}_2=\lambda_2 \textbf{x}_2$ 成立
- $\textbf{x}_1^T\boldsymbol{A}=\lambda_1 \textbf{x}_1^T$
- $\textbf{x}_1^T\boldsymbol{A}\textbf{x}_2=\lambda_1 \textbf{x}_1^T\textbf{x}_2=\lambda_2\textbf{x}_1^T\textbf{x}_2$
- $(\lambda_1-\lambda_2)\textbf{x}_1^T\textbf{x}_2=0$,因此 $\textbf{x}_1$ 与 $\textbf{x}_2$ 正交
性质3:实对称矩阵相同特征值所对应的特征向量必定线性无关。- 证明较繁琐,不详细展开
- 线性无关的向量可以通过施密特正交化转为正交向量
- 对于线性无关向量组 $\textbf{x}_1,\textbf{x}_2,…,\textbf{x}_n$,转为正交向量组 $\textbf{y}_1,\textbf{y}_2,…,\textbf{y}_n$
- $\textbf{y}_1=\textbf{x}_1$
-
$\textbf{y}_i=\textbf{x}_i-\sum\limits_{j=1}^{i-1}\displaystyle\frac{\textbf{x}_i^T\textbf{y}_j}{\textbf{y}_j^T\textbf{y}_j}\textbf{y}_j$
- 由于新的正交向量都是原来线性无关向量的线性组合,而原先的线性无关向量对应的特征值均相同,因此新的正交向量也均为该相同特征值对应的特征向量
性质4:任何一个实对称矩阵,都可以正交对角化。- 正交对角化,即存在一个正交矩阵 $\boldsymbol{Q}(\boldsymbol{Q}^T=\boldsymbol{Q}^{-1})$ 使得 $\boldsymbol{Q}^T\boldsymbol{A}\boldsymbol{Q}=\boldsymbol{D}$,其中 $\boldsymbol{D}$ 是一个对角矩阵
- 实对称矩阵,一定有 $n$ 个解,因为实对称矩阵特征值都是实数,因此一共有 $n$ 个实特征值(包括重特征值)—— 性质 $1$
- 不同特征值对应的特征向量正交,相同特征值也一定存在对应的正交向量 —— 性质 $2,3$
- 实对称矩阵,一定有 $n$ 个正交特征向量,因此可以特征值分解,即该性质成立
性质5:实对称矩阵的非零特征值个数等于矩阵的秩- 矩阵 $\boldsymbol{A}$ 相似于对角矩阵,$\boldsymbol{P}^{-1}\boldsymbol{A}\boldsymbol{P}=\boldsymbol{D}$
- 对角矩阵 $\boldsymbol{D}$ 的秩 = 矩阵 $\boldsymbol{A}$ 的秩 = $\boldsymbol{D}$ 非零特征值个数
- 矩阵 $\boldsymbol{A}$ 与 矩阵 $\boldsymbol{D}$ 相似,则特征值相同
性质6:实对称矩阵不一定可逆,但若可逆,则一定是实对称矩阵- 0 矩阵对称不可逆
- $(A^{-1})^T=(A^T)^{-1}=A^{-1}$
矩阵特征值分解
1. 概念
$n*n$ 的方阵 $\boldsymbol{A}$,由 $\boldsymbol{A}\textbf{x}=\lambda \textbf{x}$ 可以得到 $\boldsymbol{A}\boldsymbol{V}=\boldsymbol{V}\Lambda$。
-
如果方阵 $\boldsymbol{A}$ 有 $n$ 个线性无关的特征向量,则 $\boldsymbol{V}$ 可逆
-
$\boldsymbol{A}=\boldsymbol{V}\Lambda\boldsymbol{V}^{-1}$
-
其中矩阵 $\boldsymbol{V}$ 的列为方阵 $\boldsymbol{A}$ 的特征向量,$\Lambda=diag(\lambda_1,\lambda_2,…,\lambda_n),\lambda_i\geq \lambda_{i+1}$
矩阵 SVD 分解
1. 概念
任意一个矩阵 $\boldsymbol{A}$ 都可以分解为 $\boldsymbol{A}=\boldsymbol{U}\Sigma\boldsymbol{V}^T$,其中 $\boldsymbol{U},\boldsymbol{V}$ 均为正交单位矩阵,$\Sigma$ 为对角矩阵。
2. 证明
-
$\boldsymbol{A}^T\boldsymbol{A}=(\boldsymbol{U}\Sigma\boldsymbol{V}^T)^T\boldsymbol{U}\Sigma\boldsymbol{V}^T=\boldsymbol{V}\Sigma^2\boldsymbol{V}^T$,由于 $\boldsymbol{A}^T\boldsymbol{A}$ 为实对称矩阵,因此 $\boldsymbol{V}$ 为矩阵 $\boldsymbol{A}^T\boldsymbol{A}$ 对应特征向量组成的正交单位阵。
-
$\boldsymbol{A}\boldsymbol{A}^T=\boldsymbol{U}\Sigma\boldsymbol{V}^T(\boldsymbol{U}\Sigma\boldsymbol{V}^T)^T=\boldsymbol{U}\Sigma^2\boldsymbol{U}^T$,由于 $\boldsymbol{A}\boldsymbol{A}^T$ 为实对称矩阵,因此 $\boldsymbol{U}$ 矩阵 $\boldsymbol{A}\boldsymbol{A}^T$ 对应特征向量组成的正交单位阵。
-
$\boldsymbol{A}\boldsymbol{V}=\boldsymbol{U}\Sigma$,其中 $\Sigma$ 为对角阵,因此 $\boldsymbol{A}\textbf{v}_i=\sigma_i\textbf{u}_i$,由此可以得到对角矩阵 $\Sigma$,其中 $\sigma_i$ 就是奇异值。
-
$\boldsymbol{A}_{m*n}=\boldsymbol{U}_{m*m}\Sigma_{m*n}\boldsymbol{V}_{n*n}^T$
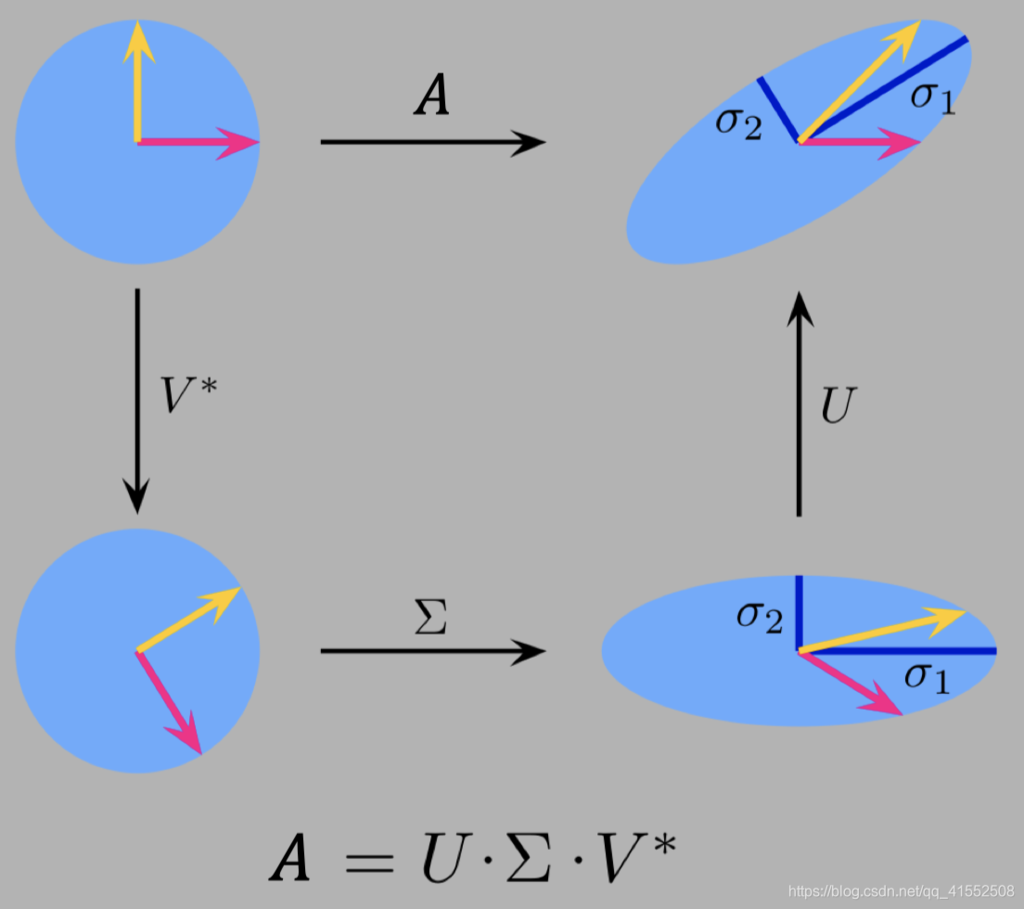
3. 几何角度
矩阵 $U,V$ 仅负责旋转,$\Sigma$ 负责放缩,具体示意图如下:
4. SVD 压缩
如下所示,仅选取前 $r$ 个不为零的奇异值,可以实现无损压缩。注意非零奇异值的个数等于矩阵 $A$ 的秩。

5. 计算伪逆

6. Eckart-Young Theorem
如果矩阵 $\mathbf{B}$ 的秩为 $k$,则 $||A-B||\geq||A-A_k||$ 对如下三个矩阵范数成立:
-
$||A||_2=\sigma_1$,即最大的奇异值
-
$||A||_{Nuclear}=\sum\limits_{i=1}^r\sigma_i$
-
Frobenius norm $=||A||_{2,1}=||A||_F=(tr(A^TA))^{1/2}=(\sum\limits_{i=1}^m\sum\limits_{j=1}^na_{ij}^2)^{1/2}$
其中 $\mathbf{A}$ 与 $\mathbf{A_k}$ 定义如下:
需要注意,矩阵乘上一个正交矩阵,其奇异值不会发生变化,即上述涉及的矩阵范数不会改变。
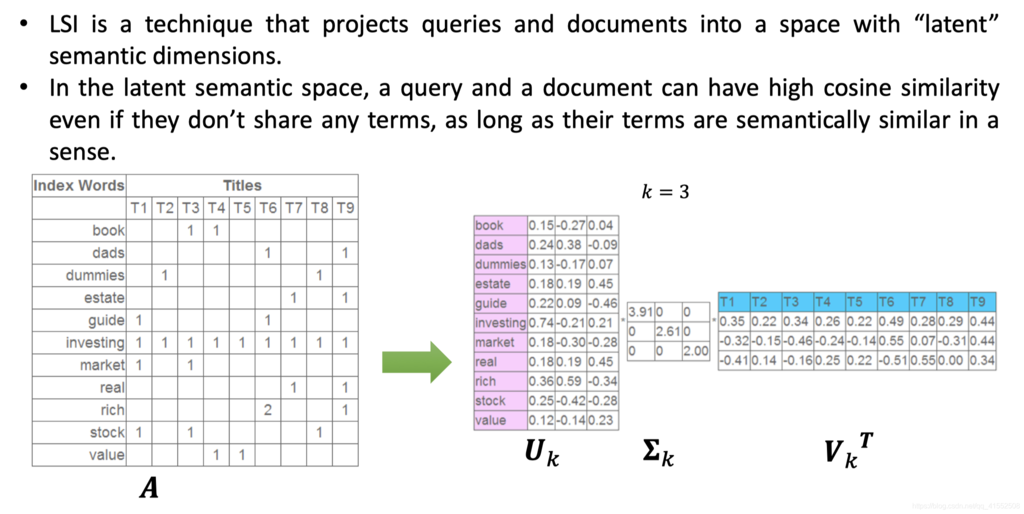
7. LSI
计算不同 $query$ 之间的相似程度,常用于推荐系统。
更多 SVD 的应用: