线性回归 (Linear Regression)
数据
-
$D=\{(\pmb{x}_1,y_1),(\pmb{x}_2,y_2),...,(\pmb{x}_m,y_m)\}$
-
$\pmb{x}_i=(x_{i1},x_{i2},...,x_{id})^T\in\mathbb{R}^d$
- $y_i\in \mathbb{R}$
模型假设
-
$\pmb{w}=(b,w_1,w_2,…,w_d)^T\in \mathbb{R}^{d+1}$
-
$\hat{\pmb{x}_i}=(1;\pmb{x}_i)\in \mathbb{R}^{d+1}$
-
$X=(\hat{\pmb{x}_1}^T;\hat{\pmb{x}_2}^T;…;\hat{\pmb{x}_m}^T)\in \mathbb{R}^{m\times(d+1)}$
-
$h(\pmb{x}_i)=\pmb{w}^T\hat{\pmb{x}_i}$
目标函数
-
$\min\ E(\pmb{w})=\sum\limits_{i=1}^m(h(\pmb{x}_i)-y_i)^2=||X\pmb w-\boldsymbol{y}||^2_2$
模型求解
-
$E(\pmb{w})$ 连续、可微且为凸函数,因此最优点 $\triangledown E(\pmb w^*)=0$
-
$E(\pmb{w})=(X\pmb w-\boldsymbol{y})^T(X\pmb w-\boldsymbol{y})=\pmb w^TX^TX\pmb w-2\pmb w^TX^T\boldsymbol{y}+\boldsymbol{y}^T\boldsymbol{y}$
-
$\triangledown E(\pmb w)=2(X^TX\pmb w-X^T\boldsymbol{y})=0$
-
$\pmb w^*=(X^TX)^{-1}X^Ty=X^{\dagger}y$
细节注意
$(X^TX)$ 若不可逆,则存在多个 $\pmb w^*$ 满足条件,此时有如下两种解决方法。
一是根据归纳偏好(例如 “奥卡姆剃刀” 原则)在多个 $\pmb w^*$ 中选择一个;二是引入正则化(regularization)项,避免不可逆的情况:
-
$\min\ E(\pmb{w})=||X\pmb w-\boldsymbol{y}||^2_2+\lambda||\pmb w||_2^2$
- $\pmb w^*=(X^TX+\lambda I)^{-1}X^Ty$
逻辑回归 (Logistic Regression)
前置知识
Sigmoid Function
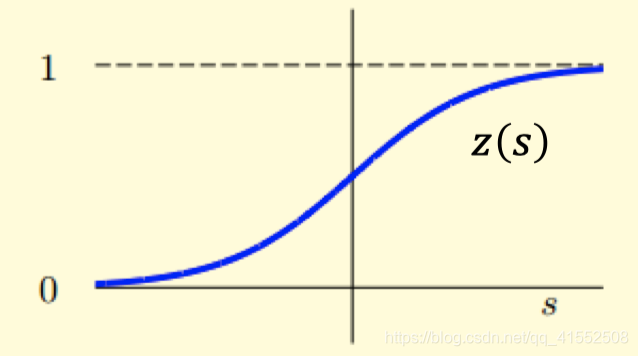
用 Sigmoid 函数对 0-1 分类函数做平滑:
-
$z(s)=\displaystyle\frac{e^s}{1+e^s}=\displaystyle\frac{1}{1+e^{-s}}$
-
$z’(s)=z(s)(1-z(s))=z(s)z(-s)$
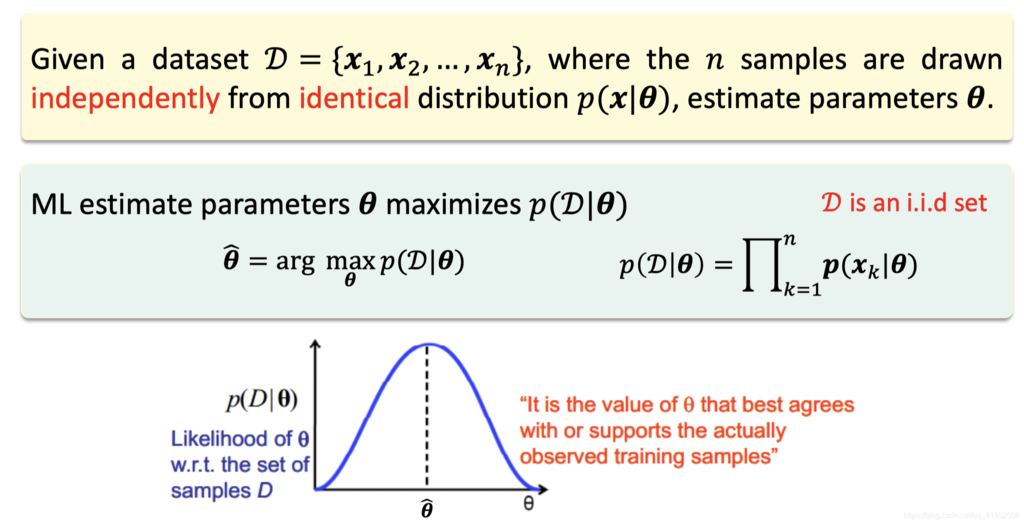
极大似然估计 (Maximum-Likelihood Estimation)
使用 Sigmoid 函数,即可得到分类器的形式,即:
此时若与线性回归一致,使用平方损失作为损失函数,则目标函数将非凸,整体计算性质不佳,无法使用各类凸优化方法进行求解。因此,在逻辑回归中,使用极大似然估计求解模型参数,即模型参数为使训练数据出现概率最高时的值。
数据
-
$D=\{(\pmb{x}_1,+),(\pmb{x}_2,-),...,(\pmb{x}_m,-)\}$
-
$\pmb{x}_i=(x_{i1},x_{i2},...,x_{id})^T\in\mathbb{R}^d$
-
$y_i\in \{0,1\}$
模型假设
-
$\pmb{w}=(b,w_1,w_2,…,w_d)^T\in \mathbb{R}^{d+1}$
-
$\hat{\pmb{x}_i}=(1;\pmb{x}_i)\in \mathbb{R}^{d+1}$
-
$X=(\hat{\pmb{x}_1}^T;\hat{\pmb{x}_2}^T;…;\hat{\pmb{x}_m}^T)\in \mathbb{R}^{m\times(d+1)}$
-
$h(\pmb{x}_i)=p(+|\pmb{x}_i)=z(\pmb{w}^T\hat{\pmb{x}_i})=\displaystyle\frac{1}{1+e^{-\textbf{w}^T\hat{\textbf{x}_i}}}$
目标函数
-
$\underset{h}{\max}\ likelihood(h)=\prod\limits_{i=1}^mp(\pmb x_i)p(y_i|\pmb x_i) \propto \prod\limits_{i=1}^m p(y_i|\pmb x_i)=\prod\limits_{i=1}^mh(\pmb x_i)^{y_i}(1-h(\pmb x_i))^{(1-y_i)}$
-
取对数再代入 $h(\pmb x_i)$ 化简
- $\underset{h}{\min} \ E(h)=\underset{\textbf w}{\min} \ E(\pmb w)= \sum\limits_{i=1}^m[-y_i\pmb w^T\pmb x_i+ln(1+e^{\textbf w^T\textbf x_i})]$
模型求解
-
$\triangledown E(\pmb w)=\sum\limits_{i=1}^m[z(\pmb w^Tx_i)-y_i]\pmb x_i$
-
无法求得 $\triangledown E(\pmb w)=0$,因此无闭式解(closed form solution)
-
使用梯度下降或牛顿迭代进行求解


优化方法
梯度下降法

牛顿法
