期望
-
$E[a]=a$
-
$E[aX]=aE[X]$
-
$E[X+Y]=E[X]+E[Y]$
-
$E[X,Y]=E[X]E[Y]$ 当且仅当 $\operatorname{Cov}[X,Y]=0$
-
$E[Y]=E[E(Y|X)]$(全期望公式)
- $E^2[XY]\leq E[X^2]E[Y^2]$(柯西-施瓦茨不等式)
方差
-
$\operatorname{Var}[a]=D[a]=0$
-
$D[aX]=a^2D[X]$
-
$D[X]=E[(X-E[X])^2]=E[X^2]-E^2[X]$
-
$D[aX+bY]=a^2D[X]+b^2D[Y]+2ab\operatorname{Cov}[X,Y]$
-
$\operatorname{Var}\left(\sum_{i=1}^{N} X_{i}\right)=\sum_{i, j=1}^{N} \operatorname{Cov}\left(X_{i}, X_{j}\right)=\sum_{i=1}^{N} \operatorname{Var}\left(X_{i}\right)+\sum_{i \neq j} \operatorname{Cov}\left(X_{i}, X_{j}\right)$
-
$\operatorname{Var}\left(\sum_{i=1}^{N} a_{i} X_{i}\right)=\sum_{i, j=1}^{N} a_{i} a_{j} \operatorname{Cov}\left(X_{i}, X_{j}\right)$,$a_i$ 为常数,$X_i$ 为随机变量
协方差
-
$\operatorname{Cov}[X,Y]=E[{X-E[X]}{Y-E[Y]}]=E[XY]-E[X]E[Y]$
-
$|\operatorname{Cov}[X,Y]|\leq \sqrt{\operatorname{Var}[X]\operatorname{Var}[Y]}$
-
若 $\operatorname{Cov}[X,Y]=0$,则 $E[XY]=E[X]E[Y]$
-
$\operatorname{Cov}[X,Y+Z]=\operatorname{Cov}[X,Y]+\operatorname{Cov}[X,Z]$
- $\operatorname{Cov}[aX,Y]=\operatorname{Cov}[X,aY]=a\operatorname{Cov}[X,Y]$
相关系数
-
$\rho(X,Y)=\displaystyle\frac{\operatorname{Cov}[X,Y]}{\sqrt{\operatorname{Var}[X]\operatorname{Var}[Y]}}$
-
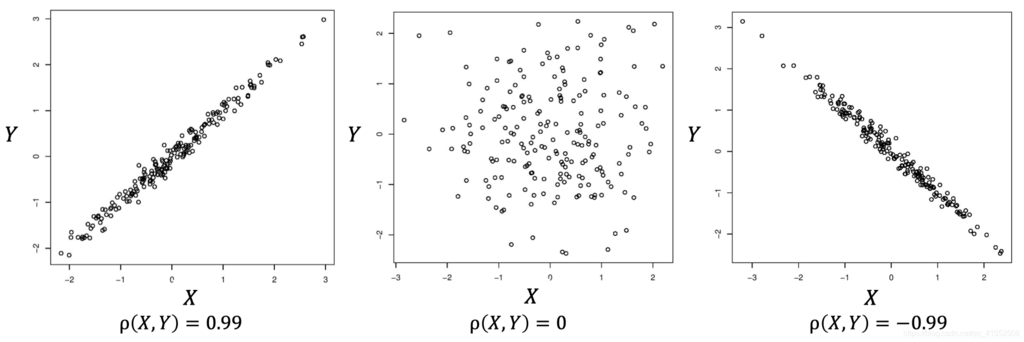
$\rho(X,Y)$ 表示 $X$ 和 $Y$ 线性关系的大小和方向,且只能反映出线性关系
-
$\rho(X,Y)=1\Longleftrightarrow$ $Y$ 随 $X$ 变大而线性增长
-
$\rho(X,Y)=-1\Longleftrightarrow$ $Y$ 随 $X$ 变小而线性下降
-
$\rho(X,Y)=0\Longleftrightarrow$ $Y$ 与 $X$ 无线性关系
-
令 $Y=a+bX+Z$,其中 $a、b$ 为常数,$Z$ 为随机变量且与 $X$ 无关
-
$\rho(X,Y)=\displaystyle\frac{b}{\sqrt{b^2+\sigma^2_Z/\sigma^2_X}}=0$,即 $b=0$
独立与不相关
-
不相关指 $\operatorname{Cov}[X,Y]=0$,即 $X$ 与 $Y$ 非线性关系,$E[XY]=E[X]E[Y]$
-
独立指 $P[XY]=P[X]P[Y]$

独立一定不相关
X,Y 为两个独立的正态分布随机变量,则协方差 $\text{Cov}(X,Y)=E[XY]-E[X]E[Y]=0$,即不相关。
不相关不一定独立
资料参考:Normally distributed and uncorrelated does not imply independent

但是当 X,Y 满足联合分布为正态分布的要求时,X,Y 不相关等价于 X,Y 独立。(证明参考)
协方差矩阵
-
$X=[X_1,X_2,…,X_n]^T$
-
$\mu=[\mu_1,\mu_2,…,\mu_n]^T$
-
$\sum=E[(X-\mu)(X-\mu)^T]$
-
对称矩阵
-
半正定矩阵,且特征值 $\geq 0$,行列式 $\geq 0$
-
$\forall y\in \mathbb{R^n},y^T\sum y=E[y^T(X-\mu)(X-\mu)^Ty]$
-
$y^T\sum y=E[((X-\mu)^Ty)^T((X-\mu)^Ty)]=E[||(X-\mu)^Ty||^2_2]\geq 0$
-
$|\sum_{ij}|\leq \sum_{ii}\sum_{jj}$
样本估计量
假设样本真实均值与方差为 $\mu,\sigma$
样本均值
样本方差
公式:
推导:
交叉验证 t 检验
原理

表格
点估计与区间估计
假设人类身高分布为正态分布,即 $X~N(\mu,\sigma^2)$。其中 $\mu$ 和 $\sigma$ 均为定值,但我们只知道 $\sigma$ 的取值,现在想要使用抽样的方法来估计 $\mu$ 的值。
假设我们抽样的数据为 $(x_1,…,x_N)$,则我们可以用这组数据的均值来估计 $\mu$,即令估计值 $\hat{\mu}=\bar{X}=\frac{1}{N}\sum_{i=1}^N x_i$,这种方法即为点估计。
点估计可以直接估计出具体数值,但对于估计误差没有度量,因此引入了区间估计的方法。
由于 $X~N(\mu,\sigma^2)$ 是确定的,因此 $\bar{X}~N(\mu,\displaystyle\frac{\sigma^2}{n})$ 也是确定的,所以我们可以得到:
由此我们可以使用区间估计,即认为 $\mu$ 在区间 $[\bar{X}-\displaystyle\frac{-1.96\sigma}{\sqrt{n}},\bar{X}+\displaystyle\frac{-1.96\sigma}{\sqrt{n}}]$ 中,并且该区间的置信度为 95%。
对置信度通常有两种理解方式:
-
$\mu$ 落在给定区间的概率为 95%
-
每抽样一次,可以得到一个区间,抽样 100 次,则可以得到 100 个区间,其中大概有 95 个区间包含 $\mu$
第二种理解方式正确,第一种则不正确,因为 $\mu$ 是定值而不是随机变量,因此 $\mu$ 要么落在区间内,要么不落在区间内,没有「概率」一说。所以通常可以将「95% 置信度」理解为「有 95% 的把握认为区间内包含 $\mu$」。