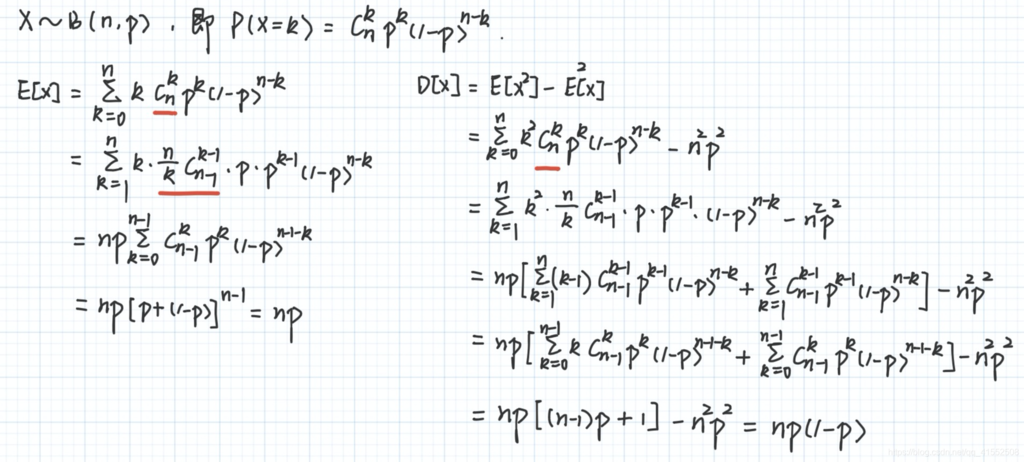一、高斯分布
1.1 一元高斯分布
-
$x\in \mathbb{R}$
-
$p(x)=\displaystyle\frac{1}{\sqrt{2\pi}\sigma}exp[-\displaystyle\frac{1}{2}(\displaystyle\frac{x-\mu}{\sigma})^2]$
1.2 多元高斯分布
-
$x\in \mathbb{R}^n$
-
$p(x)=\displaystyle\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}exp[-\displaystyle\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)]$
-
$\mu:$ Mean vector
-
$\Sigma:$ Covariance matrix
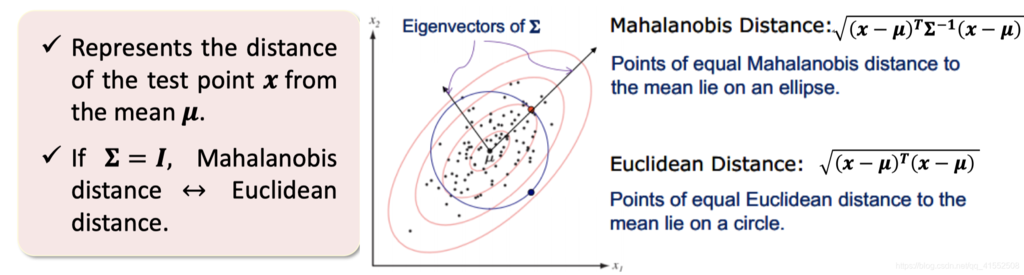
- $\sqrt{(x-\mu)^T\Sigma^{-1}(x-\mu)}:$ Mahalanobis distance
1.3 性质
- 仿射变换

- 向量子集的边缘分布

- 条件概率分布
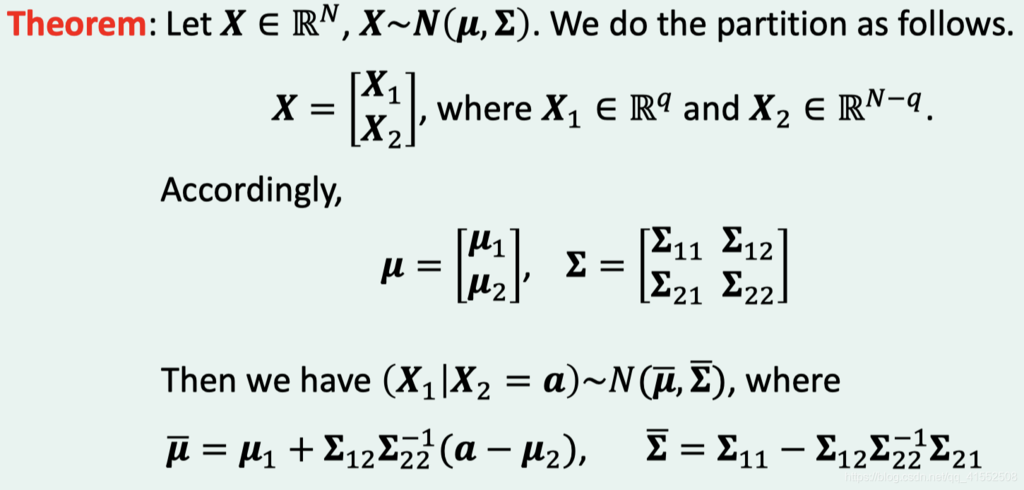
- 高斯联合分布中的变量 $x_i$ 与 $x_j$ 若不相关,则独立。
二、中心极限定理
-
$X=(X_1,X_2,…,X_n)$ 中各变量独立同分布
-
$Z=f(X)=\displaystyle\frac{1}{n}\sum\limits_{i=1}^nX_i$
-
当 $n\rightarrow\infty$,则 $p(Z)\rightarrow(E[X_i],VAR[X_i]/n)$ 的高斯分布
三、伯努利分布
概率质量函数:
$$
p(x)=\left\{\begin{aligned}& p && \text{if } x = 1 \\& 1-p && \text{if } x = 0\end{aligned}\right.\ \ \ \ \ \ \
$$
期望推导:
$$
E[X]=p+0(1-p)=p
$$
方差推导:
$$
D[X]=E[X^2]-E[X]^2=(1^2p+0^2(1-p))-p^2=p(1-p)
$$
四、二项分布