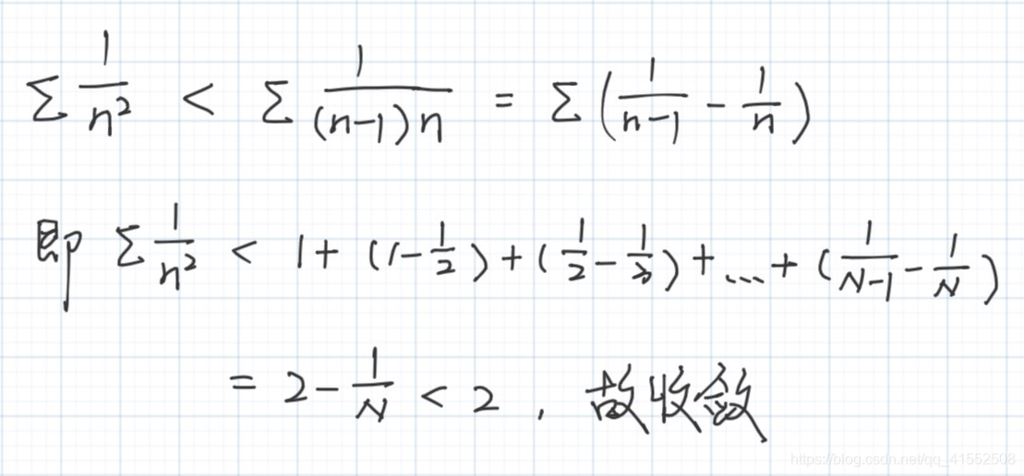一、积分坐标变换

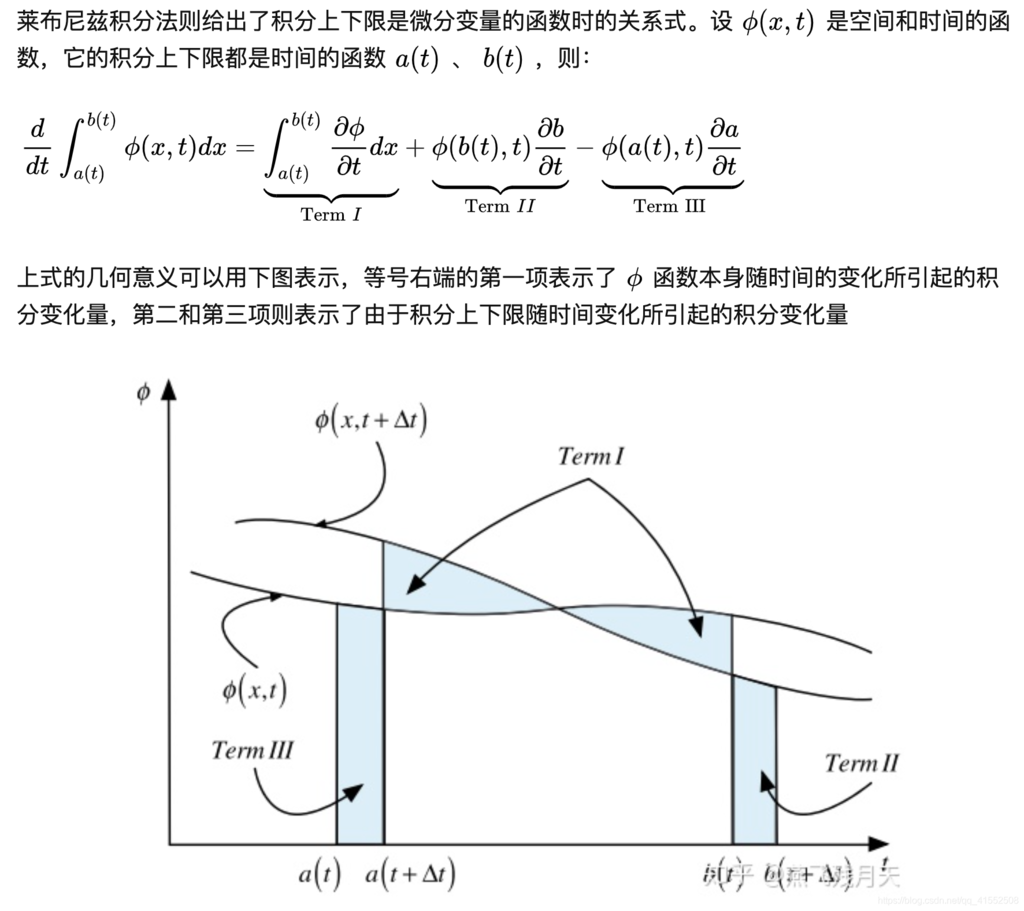
二、莱布尼兹积分法则 (Leibniz Integral Rule)
三、常见无穷级数
- $\sum\limits_{n=1}^{\infty} \displaystyle\frac{1}{n}$

- $\sum\limits_{n=1}^{\infty} \displaystyle\frac{1}{n^2}$
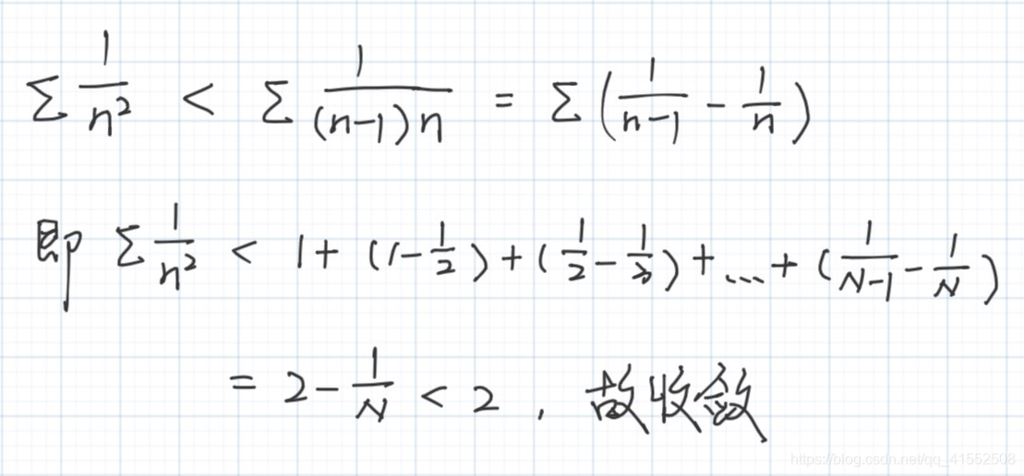
四、泰勒展开式
$$
\begin{aligned} & f(x)=\frac{f\left(x_{0}\right)}{0 !}+\frac{f^{\prime}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\ldots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+R_{n}(x) \\ & R_{n}(x)=\frac{f^{(n+1)}(\varepsilon)}{(n+1) !}\left(x-x_{0}\right)^{n+1} \end{aligned}
$$
五、导数、偏导数、方向导数、梯度
5.1 导数
$$
f^{\prime}\left(x_{0}\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta f}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)}{\Delta x}
$$
对于单一自变量,「$x_0$ 处导数」表示函数在 $x_0$ 处「关于 $x$ 轴方向的变化率」。
5.2 偏导数
$$
f_x^{\prime}\left(x_{0},y_0\right)=\lim _{\Delta x \rightarrow 0} \frac{\Delta f}{\Delta x}=\lim _{\Delta x \rightarrow 0} \frac{f\left(x_{0}+\Delta x,y_0\right)-f\left(x_{0},y_0\right)}{\Delta x}
$$
当自变量为多个时,引入偏导数概念,表示函数沿某一坐标轴的变化率。
5.3 方向导数
由于偏导数只能表示函数沿某一坐标轴的变化率,因此当我们想知道函数沿任意方向的变化率时,需要引入方向导数。
我们令二元函数 $f(x,y)$ 在 $(x_0,y_0)$ 处沿着方向 $u=\cos \theta i+\sin \theta j$ 进行求导,即:
$$
\begin{aligned} D_uf & =\lim _{t \rightarrow 0} \frac{f\left(x_{0}+t \cos \theta, y_{0}+t \sin \theta\right)-f\left(x_{0}, y_{0}\right)}{t}\\ &=\lim _{t \rightarrow 0} (\frac{f\left(x_{0}+t \cos \theta, y_{0}+t \sin \theta\right)-f\left(x_{0}, y_{0}+t \sin \theta\right)}{t}+\frac{f\left(x_{0}, y_{0}+t \sin \theta\right)-f\left(x_{0}, y_{0}\right)}{t})\\ &=\lim _{t \rightarrow 0} (\frac{f\left(x_{0}+t \cos \theta, y_{0}+t \sin \theta\right)-f\left(x_{0}, y_{0}+t \sin \theta\right)}{t\cos \theta}\cdot \cos \theta+\frac{f\left(x_{0}, y_{0}+t \sin \theta\right)-f\left(x_{0}, y_{0}\right)}{t\sin \theta }\cdot \sin \theta)\\ &=f_{x}(x_0, y_0) \cos \theta+f_{y}(x_0, y_0) \sin \theta \end{aligned}
$$
5.4 梯度
对于多元函数,存在无穷多个方向导数,因此我们希望找到某个方向,使自变量沿该方向变化,函数值增长最快。
根据之前讨论的方向导数,我们可以得知向量 $u=\cos \theta i+\sin \theta j$ 对应的导数为 $D_uf=f_{x}(x, y) \cos \theta+f_{y}(x, y) \sin \theta$。
令向量 $\nabla f=\left(f_{x}(x, y), f_{y}(x, y)\right)$,则 $D_u f$ 等于向量 $u$ 与 $\nabla f$ 的点乘,即当向量 $u$ 与 $\nabla f$ 方向一致时,函数变化率最大。
又因为 $\nabla f=\left(f_{x}(x, y), f_{y}(x, y)\right)$ 是函数增长的方向(这一点可以通过偏导数定义得到),因此 $\nabla f$ 为函数值增长最快的方向,我们将其定义为「梯度」。
六、琴生不等式 (Jensen’s Inequality)
Let $X$ be a random variable with $E(|X|)<\infty$. If $g$ is a convex function, then
$$
E[g(X)] \geq g(E(X))
$$
provided $E(|g(X)|)<\infty$. Note that if $g$ is a concave function, then the inequality will be reversed, i.e., $E[g(X)] \leq g(E(X))$. This result is readily applicable to many commonly used functions.
七、常见积分式
当 $A$ 为正定矩阵时,下式成立:
$$
\int e^{-\frac{1}{2}\left(w^T A w+b^T w+c\right)} \mathrm{d} w=\sqrt{\frac{(2 \pi)^D}{|A|}} e^{-\frac{1}{2} c+\frac{1}{8} b^T A^{-1} b}
$$
其中 $w$ 为 $D$ 维向量。