一、引入 EM
在现实应用中,除了已观测变量,还会存在隐变量,即未观测变量。
以如下一个经典例子举例:
有 3 枚硬币,分别为 A, B, C,其正面朝上概率分别是 $a,b,c$。具体实验如下:先扔硬币 A,若其为正则选硬币 B,为反则选硬币 C;再扔选出的硬币,其正反为本轮实验结果。
在这个例子中,「已观测变量」为实验结果,「未观测变量」为硬币 A 的正反面。
令 $\mathbf{X}$ 表示已观测变量集,$x_i=1$ 即表示第 $i$ 次实验结果为 $1$;$\mathbf{Z}$ 表示隐变量集,$z_i=1$ 表示第 $i$ 次实验选择了硬币 B;$\Theta$ 表示模型参数,即 ${a,b,c}$。
采用极大似然估计的思想,定义如下对数似然函数:
$$
LL(\Theta|\mathbf{X})=\ln P(\mathbf{X}|\Theta)=\ln \sum_{\mathbf{Z}}P(\mathbf{X},\mathbf{Z}|\Theta)
$$
不难发现,对数中有 $\Sigma$,因此难以对其进行最大化,由此引入 EM 算法进行计算:
$$
\begin{aligned} Q(\Theta|\Theta^t)&=\mathbb{E}_{\mathbf{Z}|\mathbf{X},\Theta^t}LL(\Theta|\mathbf{X},\mathbf {Z})\\ &=\sum_{\mathbf{Z}}P(\mathbf{Z}|\mathbf{X},\Theta^t)\ln P(\mathbf{X},\mathbf{Z}|\Theta)\\ \end{aligned}
$$
$$
\Theta^{t+1}=\mathop{\arg\max}_{\Theta} Q(\Theta|\Theta^t)
$$
不断迭代直至收敛,即可完成对参数的估计。
二、理论保证
EM 算法的每一步迭代都不会让 $LL(\Theta|\mathbf{X})$ 下降,以此达到极大似然估计的目标。
首先给出 $LL(\Theta|\mathbf{X})-LL(\Theta^t|\mathbf{X})$ 的下界:
$$
\begin{aligned} &\ \ \ \ \ LL(\Theta|\mathbf{X})-LL(\Theta^t|\mathbf{X}) \\ &=\ln \left(\sum_{\mathbf{Z}} P(\mathbf{X} | \mathbf{Z}, \Theta) P(\mathbf{Z} | \Theta)\right)-\ln P\left(\mathbf{X} | \Theta^{t}\right) \\ &= \ln \left(\sum_{\mathbf{Z}} P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right) \frac{P(\mathbf{X} | \mathbf{Z}, \Theta) P(\mathbf{Z} | \Theta)}{P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right)}\right)-\ln P\left(\mathbf{X} | \Theta^{t}\right)\\ &\geq \sum_{\mathbf{Z}} P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right) \ln \frac{P(\mathbf{X} | \mathbf{Z}, \Theta) P(\mathbf{Z} | \Theta)}{P\left(\mathbf{Z} | \mathbf{X} , \Theta^{t}\right)}-\ln P\left(\mathbf{X} | \Theta^{t}\right)\\ &=\sum_{\mathbf{Z}} P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right) \ln \frac{P(\mathbf{X} | \mathbf{Z}, \Theta) P(\mathbf{Z} | \Theta)}{P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right) P\left(\mathbf{X} | \Theta^{t}\right)} \end{aligned}
$$
上式的关键在于利用 Jensen 不等式,将 $\ln$ 函数中的 $\Sigma$ 移到了 $\ln$ 函数外,由此使 $LL(\Theta|\mathbf{X})$ 得以迭代求解。继续证明过程:
$$
LL(\Theta|\mathbf{X})\geq B(\Theta, \Theta^t)=LL(\Theta^t|\mathbf{X})+\sum_{\mathbf{Z}} P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right) \ln \frac{P(\mathbf{X} | \mathbf{Z}, \Theta) P(\mathbf{Z} | \Theta)}{P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right) P\left(\mathbf{X} | \Theta^{t}\right)}
$$
因此最大化 $LL(\Theta|\mathbf{X})$ 的过程可以转化为最大化其下界 $B(\Theta, \Theta^t)$ 的过程:
$$
\begin{aligned} \Theta^t&=\mathop{\arg\max}_{\Theta}B(\Theta, \Theta^t)\\ &=\mathop{\arg\max}_{\Theta}\sum_{\mathbf{Z}} P\left(\mathbf{Z} | \mathbf{X}, \Theta^{t}\right) \ln (P(\mathbf{X} | \mathbf{Z}, \Theta) P(\mathbf{Z} | \Theta))\\ &=\mathop{\arg\max}_{\Theta}Q(\Theta|\Theta^t) \end{aligned}
$$
由此我们可以得知 EM 算法即为「不断最大化似然函数下界」的算法,其直观理解如下:
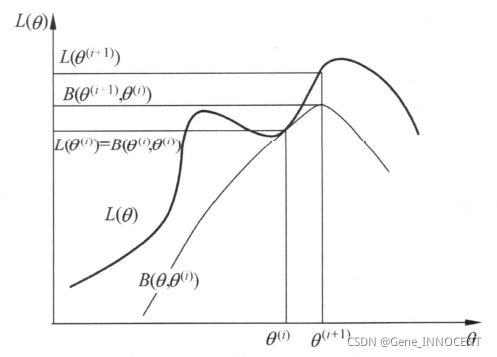
最后,需要注意,EM 算法只能保证每次迭代其似然函数值不会下降,但无法保证其能求得全局最优解。
三、GEM
通过引入隐变量的分布,我们可以得到广义 EM 的形式。首先,引入隐变量分布 $q(\mathbf{Z})$ 对 $LL(\Theta|\mathbf{X})$ 进行拆分:
$$
\begin{aligned} \ln p(\mathbf{X}|\Theta)&=\sum_{\mathbf{Z}}q(\mathbf{Z})\ln p(\mathbf{X}|\Theta) \\ &=\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\frac{p(\mathbf{X},\mathbf{Z}|\Theta)}{q(\mathbf{Z})}-\sum_{\mathbf{Z}}q(\mathbf{Z})\ln\frac{p(\mathbf{Z}|\mathbf{X},\Theta)}{q(\mathbf{Z})}\\ &=L(q,\Theta)+KL(q||p) \end{aligned}
$$
其中 $KL(q||p)\geq 0$,当且仅当 $q(\mathbf{Z})=p(\mathbf{Z}|\mathbf{X},\Theta)$ 时等号成立,具体拆分示意图如下:
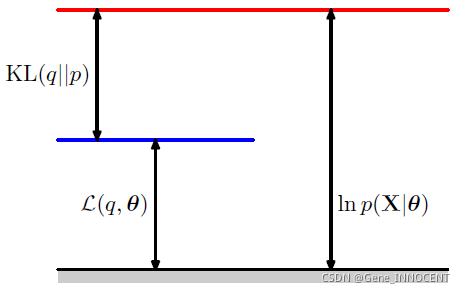
令 $q(\mathbf{Z})=p(\mathbf{Z}|\mathbf{X},\Theta^{old})$,则 $\ln p(\mathbf{X}|\Theta^{old})=L(q,\Theta^{old})$。
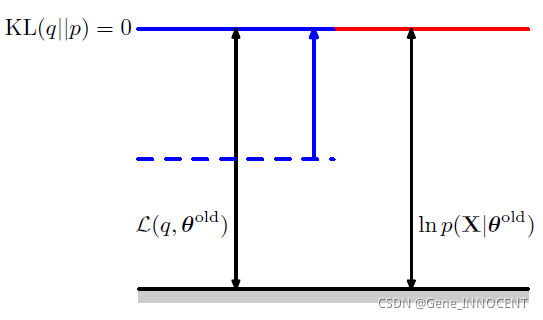
此时将 $q(\mathbf{Z})$ 代入 $L(q,\Theta)$,即可发现
$$
\begin{aligned} L(q,\Theta) &=\sum_{\mathbf{Z}} p(\mathbf{Z}| \mathbf{X},\Theta^{old}) \ln p(\mathbf{X}, \mathbf{Z} | \Theta)-\sum_{\mathbf{Z}} p(\mathbf{Z}| \mathbf{X}, \Theta^{old}) \ln p(\mathbf{Z} | \mathbf{X}, \Theta^{old}) \\ &=Q(\Theta, \Theta^{old})+\text { const } \end{aligned}
$$
再次最大化 $L(q,\Theta)$ 得到 $\Theta^{new}$,$L(q,\Theta^{new})$ 就会与 $\ln p(\mathbf{X}|\Theta^{new})$ 之间再次产生可优化的空间。
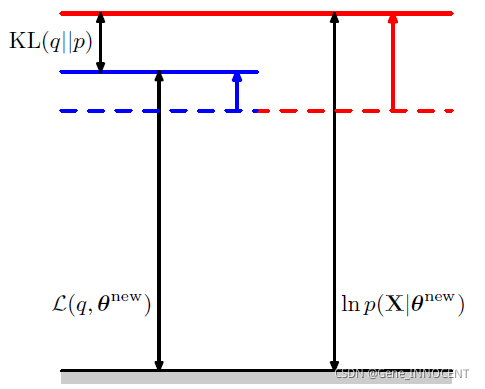
具体过程如下图所示:
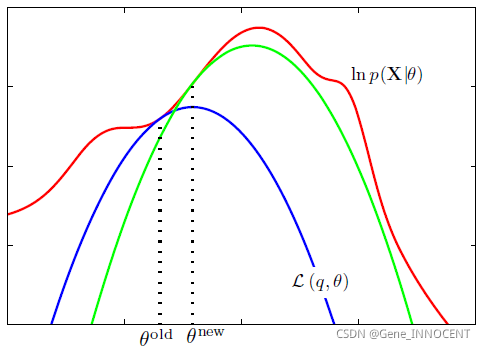
即使用 $\Theta^{old}$ 来估计 $q(\mathbf{Z})$,再根据 $q(\mathbf{Z})$ 来最大化 $L(q,\Theta)$,因此之前的 EM 算法为 GEM 的一种特例。
参考文献
-
周志华. (2016). 机器学习. 清华大学出版社, 北京.
-
李航. (2019). 统计学习方法. 清华大学出版社, 第 2 版, 北京.
-
Bishop, C.M. (2006). Pattern Recognition and Machine Learning. Springer, New York, NY.




