Supremum and Infimum
一、若函数 $f, g: A \rightarrow \mathbb{R}$ 有界,则下式成立:
$$
\begin{aligned} \left|\sup _{A} f-\sup _{A} g\right| &\leq \sup _{A}|f-g| \\ \left|\inf _{A} f-\inf _{A} g\right| &\leq \sup _{A}|f-g| \end{aligned}
$$
证明:已知 $f=f-g+g,f-g \leq|f-g|$,因此:
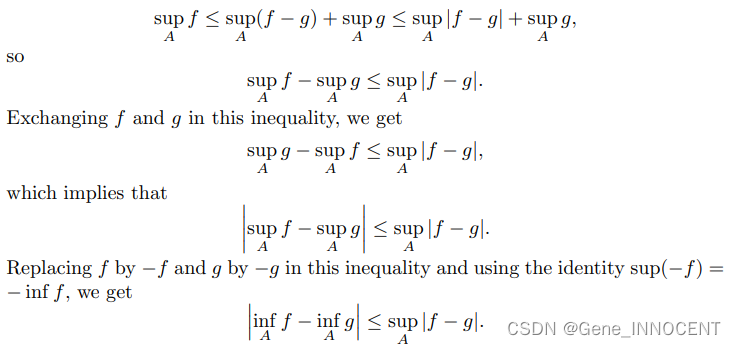
二、若有界函数 $f, g: A \rightarrow \mathbb{R}$ 满足:
$$
|f(x)-f(y)| \leq|g(x)-g(y)|, \forall x, y \in A
$$
则下式成立:
$$
\sup _{A} f-\inf _{A} f \leq \sup _{A} g-\inf _{A} g
$$
证明:
$$
\begin{aligned} f(x)-f(y) &\leq|g(x)-g(y)| \\ &=\max [g(x), g(y)]-\min [g(x), g(y)]\\ & \leq \sup _{A} g-\inf _{A} g \end{aligned}
$$
因此下式满足:
$$
\sup \{f(x)-f(y): x, y \in A\} \leq \sup _{A} g-\inf _{A} g
$$
已知 $\sup {f(x)-f(y): x, y \in A}=\sup _{A} f-\inf _{A} f$,原结论得证。
组合数
一、普通的 bound
$$
\frac{1}{n+1} 2^{n H\left(\frac{k}{n}\right)} \leqslant\left(\begin{array}{l} n \\ k \end{array}\right) \leqslant 2^{n H\left(\frac{k}{n}\right)}
$$
- 证明:信息论基础 - P201 - 例 11.1.3
二、更紧的 bound
$$
\frac{1}{\sqrt{8 n p q}} \leqslant\left(\begin{array}{c} n \\ n p \end{array}\right) 2^{-n H(p)} \leqslant \frac{1}{\sqrt{\pi n p q}}
$$
-
对于所有使 $np$ 为整数的 $0<p<1,q=1-p$ 成立
-
证明:信息论基础 - P380 - 引理 17.5.1
三、累加的 bound
对于任意 $0<\epsilon\leq \frac{1}{2}$ 和 $\eta\geq 1$,满足:
$$
\sum_{\kappa=0}^{\lfloor\epsilon \eta\rfloor}\left(\begin{array}{l} \eta \\ \kappa \end{array}\right) \leq 2^{H(\epsilon) \eta}.
$$
LogSumExp
LogSumExp 函数是一个平滑最大值,即对极值函数的光滑近似,定义如下:
$$
\operatorname{LSE}\left(x_1, \ldots, x_n\right)=\log \left(\exp \left(x_1\right)+\cdots+\exp \left(x_n\right)\right)
$$
与极值函数关系如下:
$$
\max \left\{x_1, \ldots, x_n\right\} \leq \operatorname{LSE}\left(x_1, \ldots, x_n\right) \leq \max \left\{x_1, \ldots, x_n\right\}+\log (n)
$$
另外,LSE 为凸函数,在定义域上严格递增,其凸共轭为负熵,且增加一项为零的额外参数即可定义严格凸的 LSE 函数:
$$
\operatorname{LSE}_0^{+}\left(x_1, \ldots, x_n\right)=\operatorname{LSE}\left(0, x_1, \ldots, x_n\right)
$$
计算 LSE 时,为了避免上 / 下溢,通常会使用下述等效公式:
$$
\operatorname{LSE}\left(x_1, \ldots, x_n\right)=x^*+\log \left(\exp \left(x_1-x^*\right)+\cdots+\exp \left(x_n-x^*\right)\right)
$$
其中 $x^*=\max \left\{x_1, \ldots, x_n\right\}$.