KL 散度
$KL$ 散度是一种衡量两个分布匹配程度的方法,$KL$ 散度越小,两个分布之间的匹配就越好。地址
$KL$ 散度大于等于 0,当两个分布一致时等于 0:
当分布 $p=\mathcal{N}(\mu_1,\sigma_1^2)$,$q=\mathcal{N}(\mu_2,\sigma_2^2)$ 均为高斯分布时,其 $KL$ 散度可以快速求解:
参考链接:KL divergence between two univariate Gaussians
信息熵
Entropy, in other words, is a measure of uncertainty.
其中 $\log_2(\displaystyle\frac{1}{p(x_i)})$ 可以看作是对「稀有度」的二进制编码,越「稀有」则编码长度越长。
总的来说,$H(\textbf{x})$ 衡量的是事件 $\textbf{x}$ 的期望「稀有度」编码长度,事件 $\textbf{x}$ 越稀有,则其不确定性越大,其数值也越大。
当 $\textbf{x}$ 为均匀分布时,每一种可能事件概率一致,因此不确定性最强,信息熵数值最大。
Renyi Divergence
$\alpha$-Rényi Divergence:
-
$\alpha\in [0,+\infty]$
-
$\alpha= 1,\mathrm{D}_{1}(\mathcal{P} \| \mathcal{Q})=KL(\mathcal{P} \| \mathcal{Q})=\sum_{i=1}^np_i\log\frac{p_i}{q_i}$
- $\alpha= \infty,\mathrm{D}_{\infty}(\mathcal{P} | \mathcal{Q})=\log\sup_i\frac{p_i}{q_i}$
性质:
-
$\alpha>0,\mathrm{D}_{\alpha}(\mathcal{P} | \mathcal{Q})=0$ iff $\mathcal{P}=\mathcal{Q}$
-
$\alpha=0,\mathrm{D}_{\alpha}(\mathcal{P} | \mathcal{Q})=0$ iff $\mathcal{Q}\ll\mathcal{P}$
-
$\forall \alpha\in [0,1],\mathrm{D}_{\alpha}(\mathcal{P} | \mathcal{Q})$ is jointly convex in $(\mathcal{P},\mathcal{Q})$:
-
$\forall \lambda\in (0,1),D_{\alpha}\left((1-\lambda) P_{0}+\lambda P_{1} |(1-\lambda) Q_{0}+\lambda Q_{1}\right) \leq(1-\lambda) D_{\alpha}\left(P_{0} | Q_{0}\right)+\lambda D_{\alpha}\left(P_{1} | Q_{1}\right)$
-
$\forall \alpha\in [0,\infty],\mathrm{D}_{\alpha}(\mathcal{P} | \mathcal{Q})$ is convex in $\mathcal{Q}$:
-
$\forall \lambda\in (0,1),D_{\alpha}\left(P |(1-\lambda) Q_{0}+\lambda Q_{1}\right) \leq(1-\lambda) D_{\alpha}\left(P | Q_{0}\right)+\lambda D_{\alpha}\left(P | Q_{1}\right)$
-
$\forall \alpha\in [0,\infty],\mathrm{D}_{\alpha}(\mathcal{P} | \mathcal{Q})$ is jointly quasi-convex in $(\mathcal{P},\mathcal{Q})$:
-
$\forall \lambda\in (0,1),D_{\alpha}\left((1-\lambda) P_{0}+\lambda P_{1} \|(1-\lambda) Q_{0}+\lambda Q_{1}\right) \leq \max \left\{D_{\alpha}\left(P_{0} \| Q_{0}\right), D_{\alpha}\left(P_{1} \| Q_{1}\right)\right\}$
-
三角不等式,其中 $\mathrm{d}_{\alpha}(\mathcal{P} \| \mathcal{Q})=\exp({\mathrm{D}_{\alpha}(\mathcal{P} \| \mathcal{Q})})$
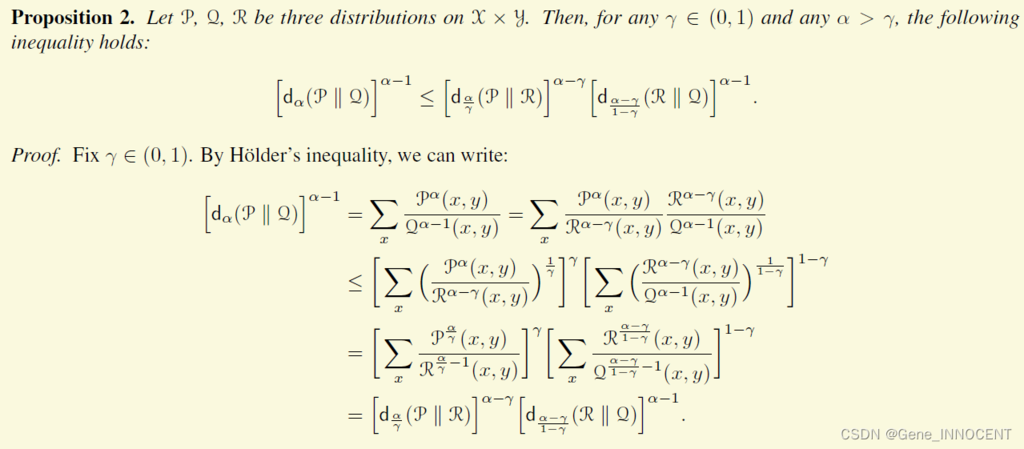
参考资料:
香农定理
- 香农第一定理
- 来自 $X$ 的 $n$ 个字符,若每个字符独立同分布,则:
$$ H(X) \leq L_{n}<H(X)+\frac{1}{n} $$- 若不满足独立同分布条件,则用熵率来约束:
$$ \frac{H\left(X_{1}, X_{2}, \ldots, X_{n}\right)}{n} \leq L_{n}^{*}<\frac{H\left(X_{1}, X_{2}, \ldots, X_{n}\right)}{n}+\frac{1}{n} $$ -
-
定理内容:对于离散无记忆信道,小于信道容量 $C$ 的所有码率都是可达的。具体来说,对任意码率 $R<C$,存在一个 $(2^{nR},n)$ 码序列,它的最大误差概率为 $\lambda^{(n)}\rightarrow 0$。反之,任意满足 $\lambda^{n}\rightarrow 0$ 的 $(2^{nR},n)$ 码序列必定有 $R\leq C$。
-
定理意义:信道容量 $C$ 是可达码率 $R$ 的上确界。
-