三对角行列式
$$
D_{n}=\left|\begin{array}{ccccccc} b & c & 0 & \ldots & 0 & 0 & 0 \\ a & b & c & \ldots & 0 & 0 & 0 \\ 0 & a & b & \ldots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & 0 & 0 & \ldots & a & b & c \\ 0 & 0 & 0 & \ldots & 0 & a & b \end{array}\right|
$$
不动点定理
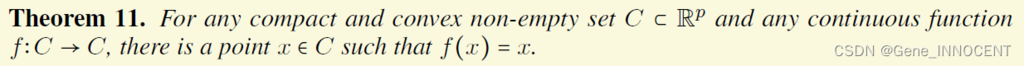
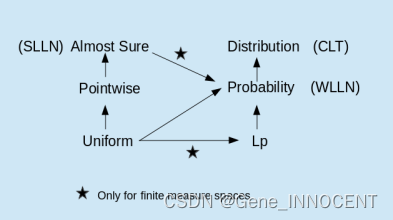
各类收敛定义及性质
Theorem、Proposition、Lemma、Corollary 等区别
-
「Theorem」:定理,是文章中重要的数学化的论述,一般有严格的数学证明。
-
「Proposition」:命题,经过证明且 interesting,但没有 Theorem 重要,比较常用。
-
「Lemma」:一种比较小的定理,通常 Lemma 的提出是为了来逐步辅助证明 Theorem,有时候可以将 Theorem 拆分成多个小的 Lemma 来逐步证明,以使得证明的思路更加清晰。很少情况下 Lemma 会以其自身的形式存在。
-
「Corollary」:推论,由 Theorem 推出来的结论,通常我们会直接说 this is a corollary of Theorem A。
-
「Property」:性质,结果值得一记,但是没有 Theorem 深刻。
-
「Claim」:陈述,先论述然后会在后面进行论证,可以看作非正式的 Lemma。
-
「Note」:注解。
-
「Remark」:涉及到一些结论,相对而言,Note 像是说明,而 Remark 则是非正式的定理。
-
「Conjecture」:猜测,一个未经证明的论述,但是被认为是真。
-
「Axiom / Postulate」:公理,不需要证明的论述,是所有其他 Theorem 的基础。