机器学习算法 - 博客收藏

“Everything should be made as simple as possible but no simpler”, Albert Einstein

1. 算法详解

1.1 谱聚类

对比传统聚类算法 K-Means，谱聚类对数据分布的适应性更强，聚类效果也更好，且计算量较小，实现也不复杂，是广泛使用的聚类算法。

参考资料：

• 谱聚类（spectral clustering）原理总结

1.2 EM 算法

EM 算法理解的九层境界：

1. EM 就是 E + M
2. EM 是一种局部下限构造
3. K-Means 是一种 Hard EM 算法
4. 从 EM 到广义 EM
5. 广义 EM 的一个特例是 VBEM
6. 广义 EM 的另一个特例是 WS 算法
7. 广义 EM 的再一个特例是 Gibbs 抽样算法
8. WS 算法是 VAE 和 GAN 组合的简化版
9. KL 距离的统一

参考资料：

• EM 算法解析

• EM 算法理解的九层境界

1.3 Isolation 系列

孤立核 (Isolation Kernel)：

• 基于数据分布特性的核函数，即增加低密度区域里物体的相似度，降低高密度区域里物体的相似度

孤立森林 (Isolation Forest)：

• 异常检测算法，寻找分布稀疏且离密度高的群体较远的点

• 算法核心：随机划分多次，密度越疏的簇，即更有可能是异常值的点会被更快地划分出来

参考资料：

• 孤立森林（iForest - Isolation Forest）

• 孤立核函数（ Isolation Kernel）的前世今生

• iForest （Isolation Forest）孤立森林 异常检测 入门篇

1.4 核密度估计

核密度估计是对直方图的一个自然扩展：

参考资料：

• Introduction to Kernel Density Estimation

• 什么是核密度估计？如何感性认识？

1.5 Optimal Transport

给定 $\mathbf{r}\in \mathbb{R}^n$、$\mathbf{c}\in \mathbb{R}^m$、$\mathbf{M}\in \mathbb{R}^{n\times m}$，我们的目标是将 $\mathbf{r}$ 变换至 $\mathbf{c}$，其中 $\mathbf{M}_{ij}$ 表示 $\mathbf{r}_i$ 运输到 $\mathbf{c}_j$ 的代价，因此解空间为：

此时，如果考虑 Wasserstein distance，则优化问题如下：

易知，上述优化问题为线性规划问题，其中最优解 $d_{\mathbf{M}}(\mathbf{r}, \mathbf{c})$ 即为 Wasserstein distance。如果考虑 Sinkhorn distance，即希望分配矩阵 $\mathbf{P}$ 更加均匀，则优化问题如下：

其中 $\sum_{i j}\left(\mathbf{P}_\lambda^*\right)_{i j} \mathbf{M}_{i j}$ 为 Sinkhorn distance。另外，该形式下问题有更高效的求解方式，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def compute_optimal_transport(M, r, c, lam, epsilon=1e-5):
    """
    Computes the optimal transport matrix and Slinkhorn distance using the
    Sinkhorn-Knopp algorithm

    Inputs:
        - M : cost matrix (n x m)
        - r : vector of marginals (n, )
        - c : vector of marginals (m, )
        - lam : strength of the entropic regularization
        - epsilon : convergence parameter

    Output:
        - P : optimal transport matrix (n x m)
        - dist : Sinkhorn distance
    """
    n, m = M.shape
    P = np.exp(- lam * M)
    # Avoiding poor math condition
    P /= P.sum()
    u = np.zeros(n)
    # Normalize this matrix so that P.sum(1) == r, P.sum(0) == c
    while np.max(np.abs(u - P.sum(1))) > epsilon:
        # Shape (n, )
        u = P.sum(1)
        P *= (r / u).reshape((-1, 1))
        P *= (c / P.sum(0)).reshape((1, -1))
    return P, np.sum(P * M)

另外，根据 Wasserstein distance，还可以定义 Wasserstein Barycenter 的概念，可以理解为 Wasserstein 距离度量下的质心。具体来说，给定一组分布 $\mathcal{P}=\left\{p_1, p_2, \cdots, p_K\right\}$，其 Wasserstein barycenter 定义为：

其中 $W$ 表示 Wasserstein distance，$\mathcal{Q}$ 表示概率分布空间，$\lambda_k$ 满足 $\sum_{k=1}^K \lambda_k=1$。

相关资料：

• Python Package - POT

• Optimal Transport 入门简述 - 博客

• Optimal Transport 入门简述 - 代码

• 令人拍案叫绝的Wasserstein GAN

• Wasserstein Distance - 数学

• Learning with a Wasserstein Loss

• A user’s guide to optimal transport

• 王祥丰：计算最优传输及其应用浅谈

• 计算最优传输系列文章

1.6 Diffusion Models - DDPM

Diffusion Models 功能：一个生成器，通过对一堆已有图片进行学习，使其可以源源不断生成大量的新图片，即通过 $p_{\text{data}}$ 学习 $p_\theta$，再用 $p_\theta$ 不断生成新图片。

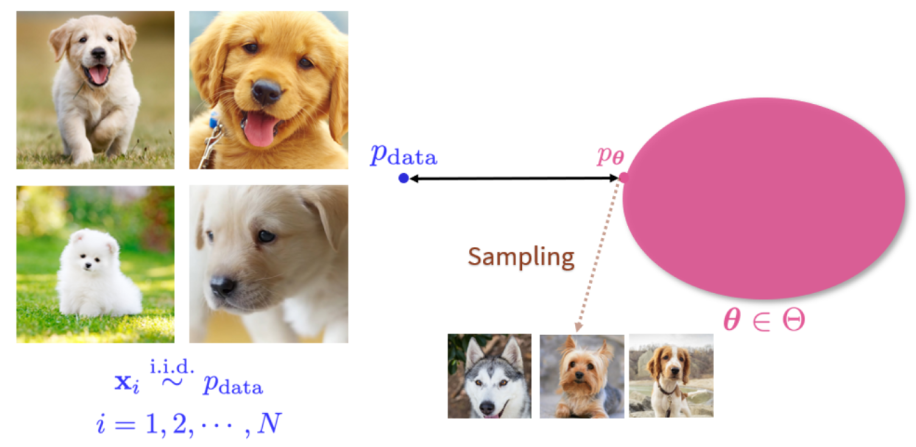
具体原理：

• 正向过程 $\mathbf{x}_0$ 到 $\mathbf{x}_T$ 的转移分布为正态分布，其均值和方差固定，使原始图片 $\mathbf{x}_0$ 通过不断加噪声，最终变成一张被噪声充斥的图片；

• 逆向过程，需要采用极大似然估计的方式，使用网络估计前向过程加随机噪声的方式，训练得到一个能估计每一步如何加噪声的网络，由此实现将 $\mathbf{x}_T$ 逆向还原为 $\mathbf{x}_0$ 的过程。

相关资料：

• 组会分享：生成扩散概率模型简介 Diffusion Models

• Diffusion Models：生成扩散模型

1.7 kd 树

机器学习中常见算法 k-NN，其原理是将 $d$ 维数据映射到 $d$ 维空间中，并根据最近的 $k$ 个点的 label 进行投票，得到预测数据的 label。

在上述过程中，「寻找最近的 $k$ 个点」成为主要难点，最常用的方式是基于 kd 树，对平面进行划分，由此高效地定位预测点在平面中的位置，实现高效查询。

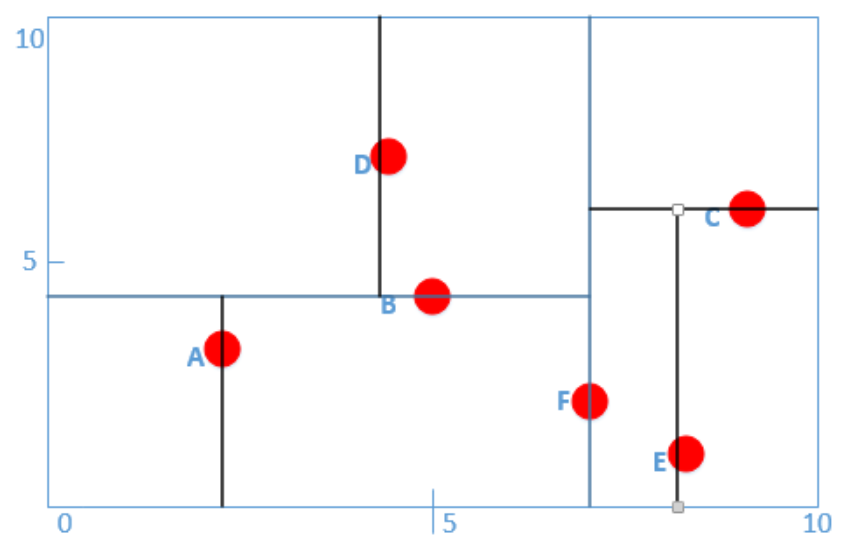
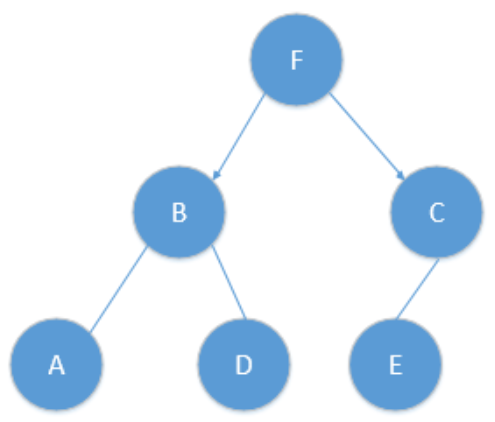
1. 通过平面划分的方式构建一棵树
2. 对于任意一个待预测点 $X$，先遍历树从上至下找到底部（例如上图 $A$），记此时距离为最近距离 $r$
3. 随后往上回溯（例如从 $A$ 回溯至 $B$），若距离更近则更新 $r$，更新完后判断以 $X$ 为中心，$r$ 为半径的球是否与 $B$ 的超平面相交
   • 如果不相交，则继续向上回溯，直至树根停止；
   • 如果相交，则进入 B 的另一部分子树，重新执行 2、3 步骤。

参考资料：

• 一文搞懂k近邻（k-NN）算法（二）

2. 精品文章收藏

• AI 算法竞赛系列 - 训练 / 测试集分布不一致解法总结

• 零知识证明：高效地验证任何类型的计算已经正确运行

  • 零知识证明（Zero-Knowledge Proof）原理介绍：在不揭晓我所知道或拥有的某样东西的前提下，向别人证明我有很大几率（这点很重要，零知识证明说到底是一个概率上的证明）确实知道或拥有这个东西。
  • Delta：开箱即用的区块链隐私计算框架、数据交易的最后一块拼图：零知识证明：对于隐私计算数据交易中的两个可信性问题（计算过程可信和原始数据可信），零知识证明技术可以实现对计算过程的验证，以及对原始数据的溯源。

• Previous
  各类数学知识记录
• Next
  机器学习讲座记录