机器学习中常见性能度量汇总

一、回归

在回归任务上，目前最常用的性能度量方式是均方误差 (Mean Squared Error, $\text{MSE}$)：

$$ \text{MSE}=\frac{1}{m}\sum_{i=1}^m (f(\boldsymbol{x}_i)-y_i)^2 $$

其余还有均方根误差 (Root Mean Squared Error, $\text{RMSE}$)：

$$ \text{RMSE}=\sqrt{\frac{1}{m}\sum_{i=1}^m (f(\boldsymbol{x}_i)-y_i)^2} $$

平均绝对误差 (Mean Absolute Error, $\text{MAE}$)：

$$ \text{MAE}=\frac{1}{m}\sum_{i=1}^m \left|f(\boldsymbol{x}_i)-y_i\right| $$

平均绝对百分比误差 (Mean Absolute Percentage Error, $\text{MAPE}$)：

$$ \text{MAPE}=\frac{100\%}{m}\sum_{i=1}^m \left|\frac{f(\boldsymbol{x}_i)-y_i}{y_i}\right| $$

对称平均绝对百分比误差 (Symmetric Mean Absolute Percentage Error, $\text{SMAPE}$)：

$$ \text{SMAPE}=\frac{100\%}{m}\sum_{i=1}^m \left|\frac{f(\boldsymbol{x}_i)-y_i}{(|f(\boldsymbol{x}_i)|+|y_i|)/2}\right| $$

加权平均绝对百分比误差 (Weighted Mean Absolute Percentage Error, $\text{WMAPE}$)：

$$ \text{WMAPE}= \frac{\sum_{i=1}^m |f(\boldsymbol{x}_i)-y_i|}{\sum_{i=1}^m y_i} $$

$\text{R-squared}$ 又称决定系数 (Coefficient of Determination)，在统计学中用于度量因变量的变异中可由自变量解释部分所占的比例，以此来判断回归模型的解释力：

$$ \text{R}^2=1-\frac{\text{MSE}}{\text{Var}}=1-\frac{\sum_{i=1}^m (f(\boldsymbol{x}_i)-y_i)^2}{\sum_{i=1}^m (\bar{y}-y_i)^2} $$

该数值越大越好，但当数据分布方差较大时，即使预测不准，$\text{R}^2$ 依然较大，此时该评价指标效果就不太好。

二、分类

在分类任务上，最常用的性能度量方式是错误率 (Error Rate, $\text{Err}$) 与精度 (Accuracy, $\text{Acc}$)，其同时适用于二分类与多分类：

$$ \begin{gathered} \text{Err} = \frac{1}{m}\sum_{i=1}^m \mathbb{I}(f(\boldsymbol{x}_i)\neq y_i) \\ \text{Acc} = 1-\text{Err} = \frac{1}{m}\sum_{i=1}^m \mathbb{I}(f(\boldsymbol{x}_i)=y_i) \end{gathered} $$

2.1 二分类

2.1.1 P-R 曲线

在信息检索、Web 搜索等应用中，我们会更关心查准率、查全率等相关指标，由此引出混淆矩阵 (Confusion Matrix)，具体定义如下所示：

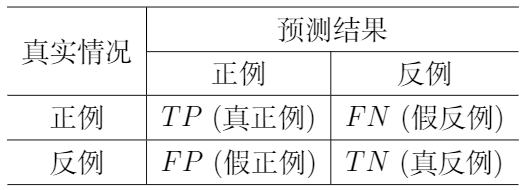
依据混淆矩阵，我们可以定义查准率 (Precision, $\text{P}$)、查全率 (Recall, $\text{R}$)：

$$ \begin{gathered} \text{P} =\frac{\text{TP}}{\text{TP}+\text{FP}} = \text{分类正确的正样本} \ / \ \text{预测为正的样本数} \\ \text{R} =\frac{\text{TP}}{\text{TP}+\text{FN}} = \text{分类正确的正样本} \ / \ \text{正样本总数} \\ \end{gathered} $$

当分类器的置信度不同时，其对应的 $\text{P}$ 与 $\text{R}$ 也会发生变化，因此很自然地可以引出 $\text{P-R}$ 曲线，其中横轴为查全率，纵轴为查准率，而平衡点 (Break-Even Point, $\text{BEP}$) 即为 $\text{P} = \text{R}$ 时的取值。

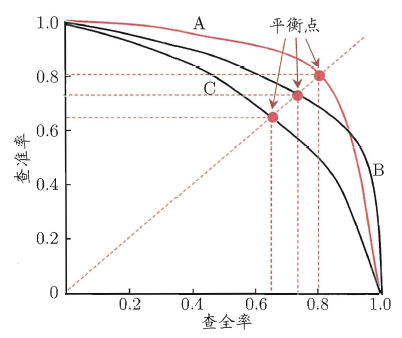
进一步地，我们可以对 $\text{P}$、$\text{R}$ 进行加权，即定义 $\text{F}1\text{-}score$ ($\text{F}1$)、$\text{F}\beta$-score ($\text{F}\beta$)，其中 $\beta>0$ 度量了查全率对查准率的相对重要性，当 $\beta>1$ 时查全率有更大影响，当 $\beta<1$ 时查准率有更大影响。

$$ \begin{gathered} \text{F}1=\frac{2\times \text{P}\times \text{R}}{\text{P}+\text{R}} \\ \text{F}_\beta = \frac{(1+\beta^2)\times \text{P}\times \text{R}}{(\beta^2 \times \text{P}) + \text{R}} \end{gathered} $$

2.1.2 ROC 曲线

在许多关注排序本身质量的应用中，$\text{AUC}$ (Area Under ROC Curve) 是一种常见的指标，其数值为 ROC 曲线下的面积。ROC 曲线以假正例率 (False Positive Rate, $\text{FPR}$) 为横轴，以真正例率 (True Positive Rate, $\text{TPR}$, 等价于召回率 $\text{R}$) 为纵轴，如下所示：

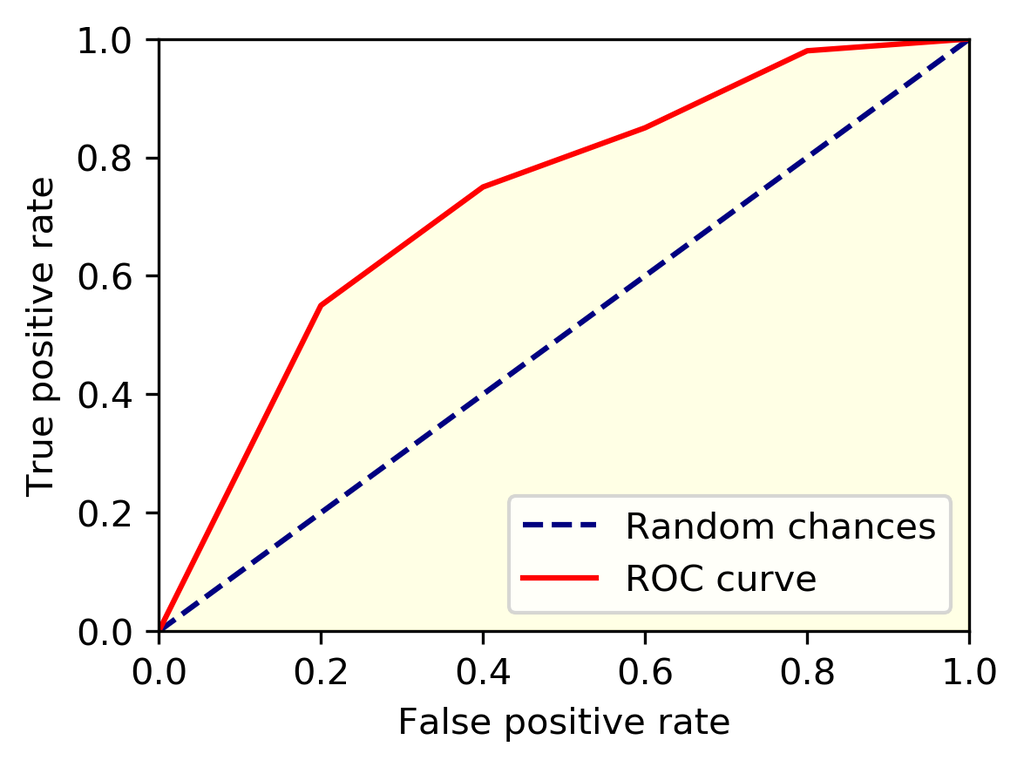
$$ \begin{gathered} \text{TPR} =\text{R}=\frac{\text{TP}}{\text{TP}+\text{FN}} = \text{分类正确的正样本} \ / \ \text{正样本总数} \\ \text{FPR} =\frac{\text{FP}}{\text{TN}+\text{FP}} = \text{分类错误的负样本} \ / \ \text{负样本总数} \\ \end{gathered} $$

计算上述 ROC 曲线下的面积，即可得到 $\text{AUC}$，其物理意义为「一个随机正样本，其排序位置高于一个随机负样本的概率」，具体计算过程如下：

$$ \begin{aligned} \text{AUC}&=\int_{+\infty}^{-\infty} \operatorname{TPR}(t) d \mathrm{FPR}(t)\ \ \ [\text{t is threshold}] \\ &=\operatorname{Pr}\left(f\left(\mathbf{x}^{+}\right)>f\left(\mathbf{x}^{-}\right)\right) \\ &= \frac{1}{m^+m^-}\sum_{\mathbf{x}^{+}\in D^+}\sum_{\mathbf{x}^{-}\in D^-} \mathbb{I}\left(f\left(\mathbf{x}^{+}\right)>f\left(\mathbf{x}^{-}\right)\right) \end{aligned} $$

2.2 多分类

在多分类任务上，通常会对应 $n$ 个混淆矩阵，此时可以直接对各混淆矩阵求均值，定义宏查准率 ($\text{macro-P}$)、宏查全率 ($\text{macro-R}$) 以及宏 $\text{F}1$ ($\text{macro-F}1$):

$$ \begin{gathered} \text {macro-P}=\frac{1}{n} \sum_{i=1}^{n} \text{P}_{i} \\ \text {macro-R}=\frac{1}{n} \sum_{i=1}^{n} \text{R}_{i} \\ \text {macro-F}1=\frac{2 \times \text {macro-P} \times \text {macro-R} }{\text {macro-P} +\text {macro-R} } \end{gathered} $$

也可以先对混淆矩阵中各元素求平均，得到 $\text{TP}$、$\text{FP}$、$\text{TN}$、$\text{FN}$ 的均值 $\overline{\text{TP}}$、$\overline{\text{FP}}$、$\overline{\text{TN}}$、$\overline{\text{FN}}$，进而定义微查准率 ($\text{micro-P}$)、微查全率 ($\text{micro-R}$)、微 $\text{F}1$ ($\text{micro-F}1$):

$$ \begin{gathered} \text {micro-P}=\frac{\overline{\text{TP}}}{\overline{\text{TP}}+\overline{\text{FP}}} \\ \text {micro-R}=\frac{\overline{\text{TP}}}{\overline{\text{TP}}+\overline{\text{FN}}} \\ \text {micro-F}1=\frac{2 \times \text {micro-P} \times \text {micro-R}}{\text {micro-P}+\text {micro-R}} \end{gathered} $$

2.3 多标签

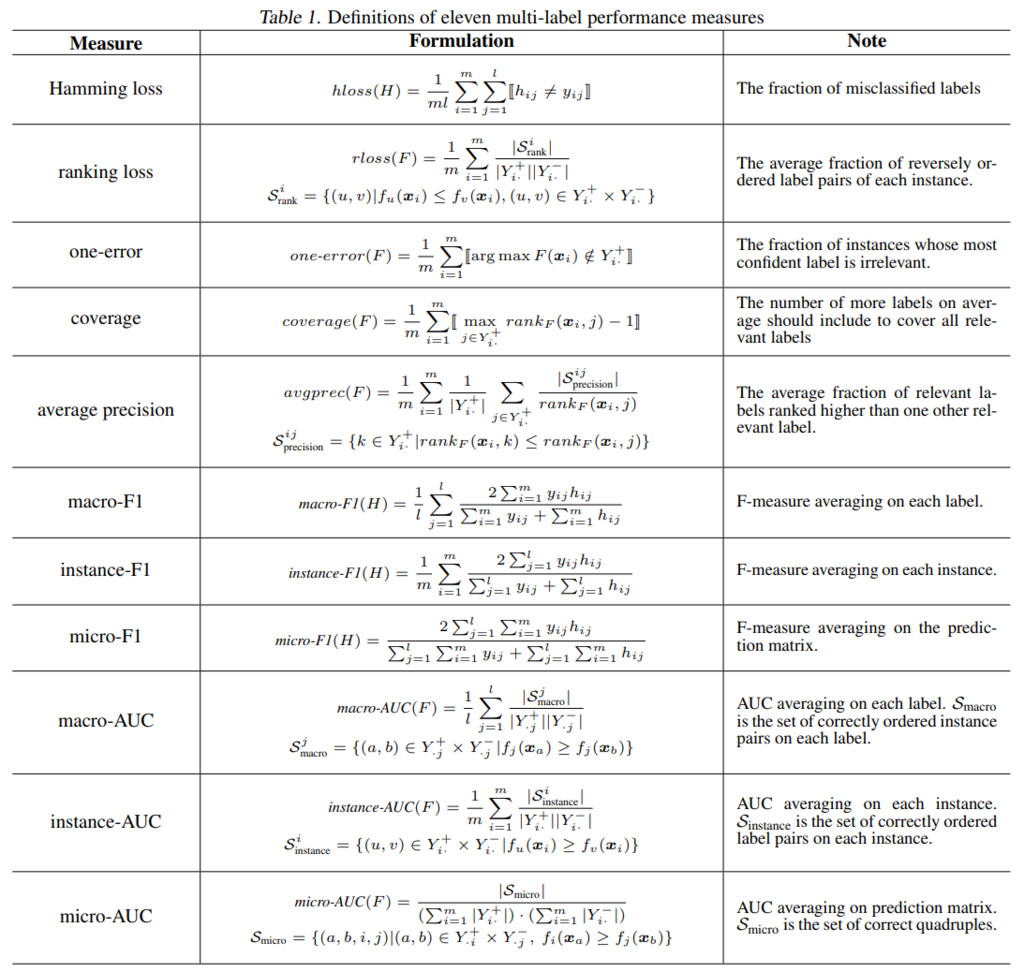
上图来自 [ICML17 - X.-Z. Wu]，其中 $y_{ij}$ 表示第 $i$ 个样本的第 $j$ 个标签，$Y_{i .}^{+}=\{j \mid y_{i j}=1\}$ 表示第 $i$ 个样本中的正类标签，$Y_{\cdot j}^{+}=\{i \mid y_{i j}=1\}$ 表示第 $j$ 个标签为正的样本。

三、排序

该部分性能度量主要与排序有关，在信息检索、推荐系统中经常使用。

3.1 F-measure

首先是 $\text{Precision}@k$ 与 $\text{Recall}@k$，在其计算中，分子均为前 $k$ 个搜索结果中相关结果的个数，但在分母上，前者为 $k$，后者则为总的相关结果个数。举个例子，假设现在搜索结果为 $[1 \ 2\ 3\ 4\ 5]$，其中 $[1\ 3\ 5]$ 为相关文档，则：

$$ \begin{aligned} \text{Precision}@\text{[1 2 3 4 5]} &=[\frac{1}{1}\ \frac{1}{2}\ \frac{2}{3}\ \frac{2}{4}\ \frac{3}{5}] \\ \\ \text{Recall}@\text{[1 2 3 4 5]} &=[\frac{1}{3}\ \frac{1}{3}\ \frac{2}{3}\ \frac{2}{3}\ \frac{3}{3}] \end{aligned} $$

由此可以直接引出 $\text{F}_\beta @k$：

$$ \text{F}_\beta @k = \frac{(1+\beta^2)\times \text{Precision}@k\times \text{Recall}@k}{(\beta^2 \times \text{Precision}@k) + \text{Recall}@k} $$

3.2 MAP

$\text{MAP}$ (Mean Average Precision) 在排序任务中使用较多，其计算主要与 $\text{P}$、$\text{R}$ 有关。首先我们需要定义 $\text{AP}$ (Average Precision)：

$$ \text{AP}=\frac{1}{m}\sum_{k=1}^n \text{P}(k) \cdot rel(k) $$

其中 $n$ 表示「搜索结果总数」，$m$ 表示「相关结果总数」，$\text{P}(k)$ 表示 $\text{Precision}@k$，$rel(k)$ 则表示第 $k$ 个搜索结果是否相关，相关为 1，否则为 0。仍使用上述例子举例，则可以得到：

$$ \text{AP}=\frac{1}{3}\cdot (\frac{1}{1}+\frac{2}{3}+\frac{3}{5}) $$

至此，可以很自然的引出 $\text{MAP}$，即 $\text{AP}$ 的平均值，其定义如下：

$$ \text{MAP}=\frac{1}{Q}\sum_{i=1}^Q \text{AP}_i $$

其中 $Q$ 表示查询的总数，$AP_i$ 表示第 $i$ 次查询的 $\text{AP}$ 值。

3.3 MRR

$\text{MRR}$ (Mean Reciprocal Rank) 即第一个相关结果排名的倒数的均值，定义如下：

$$ \text{MRR}=\frac{1}{Q}\sum_{i=1}^{Q}\frac{1}{rank_i} $$

其中 $rank_i$ 即为第 $i$ 个查询的第一个相关结果的排名。

3.4 ERR

$\text{ERR}$ (Expected Reciprocal Rank) 即用户需求被满足时停止位置的倒数的期望。相比于 $\text{MRR}$，$\text{ERR}$ 认为用户按顺序从高到低依次查看文档，一旦某个文档满足了用户的需求，则停止查看后续文档，即更加关注用户停止的位置。

为了引出 $\text{ERR}$，我们首先定义用户在位置 $r$ 停止的概率：

$$ P_r=P(\text{user stops at position }r)=R_r\prod_{i=1}^{r-1}(1-R_i) $$

其中 $R_i=\mathcal{R}(g_i)$，$g_i$ 是第 $i$ 个文档的相关度等级，而 $\mathcal{R}(\cdot)$ 则是「文档相关度等级」到「用户停止概率」的映射，其定义如下：

$$ \mathcal{R}(g)=\frac{2^g-1}{2^{g_{\max}}},g\in \{0,...,g_{\max}\} $$

举个例子，我们可以令 $g=0$ 表示文档不相关，而 $g=g_{\max}=5$ 表示文档相关度最大。至此，我们可以对 $\text{ERR}$ 进行定义：

$$ \text{ERR}=\sum_{r=1}^n\varphi(r)P_r=\sum_{r=1}^n\frac{1}{r}P_r=\sum_{r=1}^n\frac{R_r}{r}\prod_{i=1}^{r-1}(1-R_i) $$

其中 $n$ 为搜索结果总数，而 $\varphi(\cdot)$ 可以为任意满足 $\varphi(1)=1$ 且 $\varphi(r)\rightarrow0\text{ as }r\rightarrow +\infty$ 的函数形式，例如 $\varphi(r)=\frac{1}{\log_2(r+1)}$。

3.5 NDCG

与 $\text{ERR}$ 的计算过程一致，$\text{nDCG}$ 计算时也会对文档相关度分多个等级。

3.5.1 CG

$\text{CG}$ (Cumulative Gain) 表示前 $k$ 个文档相关度总和：

$$ \text{CG}@k=\sum_{i=1}^k rel_i $$

其中 $rel_i$ 表示第 $i$ 个文档的相关度等级，例如 $[-1\ 0\ 1\ 2]$ 分别表示 $[$垃圾无关相关非常相关$]$。

3.5.2 DCG

$\text{DCG}$ (Discounted Cumulative Gain) 是对 $\text{CG}$ 的进一步改进，在其基础上为每个位置赋予了不同的权重：

$$ \text{DCG}@k=\sum_{i=1}^k \varphi(i)\cdot rel_i=\sum_{i=1}^k\frac{rel_i}{\log_2(i+1)} $$

除上式外，也可以修改文档相关度的表达式，得到下述版本：

$$ \text{DCG}@k=\sum_{i=1}^k \varphi(i)\cdot (2^{rel_i}-1)=\sum_{i=1}^k\frac{2^{rel_i}-1}{\log_2(i+1)} $$

3.5.3 IDCG

$\text{IDCG}$ (Ideal DCG) 表示理想情况下的 $\text{DCG}$，即将前 $k$ 个文档根据相关度从大到小排序，得到 $\text{DCG}$ 的理想值。而 $\text{NDCG}$ 则是用 $\text{IDCG}$ 对 $\text{DCG}$ 进行归一化的结果：

$$ \text{NDCG}@k=\frac{\text{DCG}@k}{\text{IDCG}@k} $$

由于每个查询语句检索到的结果文档个数不同，因此直接使用 $\text{DCG}$ 进行比较并不恰当，因此需要对 $\text{DCG}$ 进行归一化处理，得到 $\text{NDCG}$ 后再进行比较。

参考资料

《机器学习》- 西瓜书
[ICML17 - X.-Z. Wu] A unified view of multi-label performance measures
[CIKM09 - Olivier Chapelle] Expected Reciprocal Rank for Graded Relevance