模型查搜相关研究
NCE
$\text{NCE}$ 即 Negative Conditional Entropy,其基本设定如下:
该工作利用负条件熵作为模型查搜指标,因此首先给出条件熵的定义:
$$
H(Y \mid Z)=-\sum_{y \in \mathcal{Y}} \sum_{z \in \mathcal{Z}} \hat{P}(y, z) \log \frac{\hat{P}(y, z)}{\hat{P}(z)}
$$
其具体度量的是「给定 $Z$ 后 $Y$ 的不确定性」,因此该工作的出发点是「$H(Y\mid Z)$ 越小说明 $Z$ 可能对 $Y$ 的帮助更大」。根据上述定义,我们依次对下述概率值进行估计:
$$
\begin{aligned} & \hat{P}(y, z)=\frac{1}{n} \mid\left\{i: y_i=y \text { and } z_i=z\right\} \mid \\ & \hat{P}(z)=\sum_{y \in \mathcal{Y}} \hat{P}(y, z)=\frac{1}{n}\left|\left\{i: z_i=z\right\}\right| \end{aligned}
$$
其中 $z_i=\arg \max _{z \in \mathcal{Z}} \theta\left(x_i\right)_z$(模型 $\theta$ 输出各类别的概率值),代回原式中可得:
$$
\text{NCE}=-H(Y \mid Z)=\frac{1}{n}\sum_{i=1}^n \log\hat{P}(y_i\mid z_i)
$$
因此该工作在模型查搜时,会认为 $\text{NCE}$ 指标更大的模型复用性能更强。
理论保障
将上述分类问题分为两阶段,即第一阶段为特征提取 $w: \mathcal{X} \rightarrow \mathbb{R}^D$,第二阶段为类别预测 $h: \mathbb{R}^D \rightarrow \mathcal{P}(\mathcal{Z})$,则可以定义:
$$
w_Z, h_Z=\underset{w, h \in(W, H)}{\operatorname{argmax}}\ l_Z(w, h)=\frac{1}{n} \sum_{i=1}^n \log P\left(z_i \mid x_i ; w, h\right)
$$
由于在 fine-tune 的时候,我们可以不对特征提取的部分进行改变,因此我们希望学得的目标预测器可以按下式进行定义:
$$
k_Y=\underset{k \in K}{\operatorname{argmax}}\ l_Y\left(w_Z, k\right)
$$
此时有如下理论保障:
$$
\begin{aligned} l_Y\left(w_Z, k_Y\right)& \geq l_Z\left(w_Z, h_Z\right)-H(Y \mid Z) \\ &=l_Z\left(w_Z, h_Z\right)+\text{NCE} \\ \end{aligned}
$$
因此可以从理论上说明 $\text{NCE}$ 越大,$l_Y\left(w_Z, k_Y\right)$ 的下界会更大。
局限性
LEEP
$\text{LEEP}$ 即 Log Expected Empirical Prediction,与 $\text{NCE}$ 的整体设定一致,在一些细节上做了一点修改:
$$
\begin{aligned} \text{LEEP}&=\frac{1}{n} \sum_{i=1}^n \log \left(\sum_{z \in \mathcal{Z}} \hat{P}\left(y_i \mid z\right) \theta\left(x_i\right)_z\right)\\ &=\frac{1}{n} \sum_{i=1}^n \log \left(\sum_{z \in \mathcal{Z}} \hat{P}\left(y_i \mid z\right) P\left(z \mid x_i ; w_Z, h_Z\right)\right) \\ \end{aligned}
$$
其形式上与 $\text{NCE}$ 的区别,主要在于 $\text{LEEP}$ 在 $\hat{P}(y_i\mid z)$ 上对 $z$ 求了期望。那加了期望后会得到什么不一样的结果呢?关于这一点,我们得从理论保障入手进行理解。
理论保障
$$
\begin{aligned} l_Y\left(w_Z, k_Y\right)& \geq \text{LEEP} \\ &\geq l_Z\left(w_Z, h_Z\right)+\text{NCE} \\ \end{aligned}
$$
从上式可以发现,$\text{LEEP}$ 是 $l_Y\left(w_Z, k_Y\right)$ 更紧的下界,某种程度上可以更好地刻画模型复用性能。
局限性
由于只是对 $\text{NCE}$ 的一种改进,整体设置都没有变化,因此 $\text{NCE}$ 的局限都依然存在。
LogME
上述 $\text{NCE}$ 和 $\text{LEEP}$ 方法,均在「预训练模型的输出层」做文章,导致其仅适用于分类问题。针对这一点,$\text{LogME}$ (Logarithm of Maximum Evidence) 则主要关注「预训练模型的特征提取层」,认为不同预训练模型复用能力的差别,主要体现在特征提取层输出的不同。
首先介绍下 $\text{LogME}$ 方法的场景设定:
-
源域:预训练模型 $\phi$,其用途是给定输入 $x_i$,返回提取的特征 $f_i=\phi(x_i)$
-
目标域:有标记数据 $\mathcal{D}={(x_i,y_i)}_{i=1}^n$,输出空间 $\mathcal{Y} \in \mathbb{R}^{n \times K}$
解决上述问题的 trivial 想法是学习一个线性判别式模型(例如线性回归、逻辑回归)来对「似然 (likelihood)」 $p(y\mid F,w^*)$ 建模,其中 $F=[f_1;f_2;...;f_n]\in \mathbb{R}^{n\times D}$,$y=[y_1,y_2,...,y_n]\in \mathbb{R}^n$,$w^*$ 为模型学习到的最优参数。但该方法有两方面问题:
为了改进上述 trivial 想法,文中提出对「证据 (evidence)」进行建模,即使用 $w$ 的分布来刻画边缘化似然:
$$
p(y\mid F)=\int p(w)p(y\mid F,w) \mathrm{d} w
$$
注意,由于每个样本有 $K$ 个标签,因此文中对各标签分别计算 $\text{LogME}$ 后再取均值。为进一步刻画上述「证据」,文中有如下假设:
$$
\begin{aligned} p(w\mid \alpha) &= \mathcal{N}\left(0, \alpha^{-1} I\right) \\ p\left(y_i \mid f_i, w, \beta\right)&=\mathcal{N}\left(y_i \mid w^T f_i, \beta^{-1}\right) \\ \end{aligned}
$$
代入到 $p(y\mid F)$ 中,可得:
$$
\begin{aligned} p(y \mid F, \alpha, \beta) &=\int p(w \mid \alpha) p(y \mid F, w, \beta) \mathrm{d} w \\ &=\int p(w \mid \alpha) \prod_{i=1}^n p\left(y_i \mid f_i, w, \beta\right) \mathrm{d} w \\ &=\left(\frac{\beta}{2 \pi}\right)^{\frac{n}{2}}\left(\frac{\alpha}{2 \pi}\right)^{\frac{D}{2}} \int e^{-\frac{\alpha}{2} w^T w-\frac{\beta}{2}\|F w-y\|^2} \mathrm{~d} w \end{aligned}
$$
又因为当 $A$ 正定时,有下述式子成立:
$$
\int \exp\{ {-\frac{1}{2}\left(w^T A w+b^T w+c\right)}\} \mathrm{d} w=\sqrt{\frac{(2 \pi)^D}{|A|}} \exp\{ {-\frac{1}{2} c+\frac{1}{8} b^T A^{-1} b}\}.
$$
将上述式子转为对数形式,可得:
$$
\begin{aligned} \mathcal{L}(\alpha, \beta) &=\log p(y \mid F, \alpha, \beta) \\ &=\frac{n}{2} \log \beta+\frac{D}{2} \log \alpha-\frac{n}{2} \log 2 \pi \\ &-\frac{\beta}{2}\|F m-y\|_2^2-\frac{\alpha}{2} m^T m-\frac{1}{2} \log |A| \end{aligned}
$$
其中 $A=\alpha I+\beta F^T F$,$m=\beta A^{-1} F^T y$。此时再采用与极大似然估计相同的思想,通过「极大化证据」来求取 $\alpha$ 与 $\beta$,即 $\left(\alpha^*, \beta^*\right)=\arg \max _{\alpha, \beta} \mathcal{L}(\alpha, \beta)$。此时再采用交替优化的方式,即可对其进行求解:
$$
\begin{gathered} A=\alpha I+\beta F^T F, m=\beta A^{-1} F^T y, \gamma=\sum_{i=1}^D \frac{\beta \sigma_i}{\alpha+\beta \sigma_i} \\ \alpha \leftarrow \frac{\gamma}{m^T m}, \beta \leftarrow \frac{n-\gamma}{\|F m-y\|_2^2} \end{gathered}
$$
其中 $\sigma_i$ 是 $F^TF$ 的奇异值。整个算法过程如下所示:

其中步骤 10 是步骤 9 的优化版本,其优化思路是 $A=V\Lambda V^T,A^{-1}=V\Lambda^{-1}V^T$,由此避开了对 $A$ 求逆的过程。
评估指标
当模型池中有 $M$ 个预训练模型,面对目标集合 $\mathcal{D}$,$\{T_m\}_{m=1}^M$ 表示每个预训练模型复用性能的 ground-truth,$\{S_m\}_{m=1}^M$ 表示每个预训练模型的评估分数。为评价 $\{S_m\}_{m=1}^M$ 与 $\{T_m\}_{m=1}^M$ 间的相关性,文中采用了「肯德尔 $\tau$ 系数 (Kendall’s $\tau$ coefficient)」作为评估指标,即:
$$
\begin{gathered} \tau=\frac{2}{M(M-1)} \sum_{1 \leq i<j \leq M} \operatorname{sgn}\left(T_i-T_j\right) \operatorname{sgn}\left(S_i-S_j\right) \\ \operatorname{sgn} (x)= \begin{cases}-1 & \text { if } x<0 \\ 0 & \text { if } x=0 \\ 1 & \text { if } x>0\end{cases} \end{gathered}
$$
其中 $\tau\in [-1,1]$,$\tau=1$ 表明 $T$ 与 $S$ 完全一致 ($S_i>S_j \Longleftrightarrow T_i>T_j$),$\tau=-1$ 则表明二者完全不一致 ($S_i>S_j \Longleftrightarrow T_i<T_j$)。另外,$T$ 与 $S$ 间系数为 $\tau$,表明当 $S_i>S_j$ 时,有 $(\tau+1)/2$ 的概率 $T_i>T_j$。
局限性
虽然 $\text{LogME}$ 对特征层进行刻画,使其可以应用在除分类外的其它任务上,但与 $\text{NCE}$、$\text{LEEP}$ 一样,$\text{LogME}$ 依然要求目标域有标记数据。
Ranking and Tuning
该篇文章是 $\text{LogME}$ 的期刊版本,其为了提高预训练模型库利用率,提出了 $\text{Ranking and Tuning}$ 范式:
在 $\text{Ranking}$ 部分,除了重述 $\text{LogME}$ 方法,其还证明了 $\text{LogME}$ 指标无需对特征维度进行归一化,证明方式是「将特征复制多份,或对特征补零,其 $\text{LogME}$ 指标不变」。
在 $\text{Tuning}$ 部分,其首先给出了后验概率 $p(y’\mid f,F,y)\sim \mathcal{N}\left(f^T m, f^T A^{-1} f+\beta^{*-1}\right)$ 的形式(具体计算方式在后面给出),其中 $F,y$ 分别为训练集中的特征和标签,而 $f,y’$ 则为测试时给出的特征以及模型预测的标签。
因此对于 TopK 个预训练模型,每个模型都可以得到对应后验概率:
$$
p\left(y_k^{\prime} \mid f_k, F_{\phi_k}, y\right) \sim \mathcal{N}\left(f_k^T m_k, f_k^T A_k^{-1} f_k+\beta_k^{*-1}\right)
$$
同时目标模型也有后验概率:
$$
p\left(y_t^{\prime} \mid f_t, F_t, y\right) \sim \mathcal{N}\left(f_t^T m_t, f_t^T A_t^{-1} f_t+\beta_t^{*-1}\right)
$$
因此可以将后验概率作为「知识蒸馏的损失函数」,以此避开对异构模型的特征映射矩阵进行求解,其函数形式如下:
$$
L_{\text {Bayesian }}=\left\|\mathbb{E} \bar{y}^{\prime}-\mathbb{E} y_t^{\prime}\right\|_2^2=\left(\frac{1}{K} \sum_{k=1}^K f_k^T m_k-f_t^T m_t\right)^2
$$
整体的 Tuning 框架如下所示:
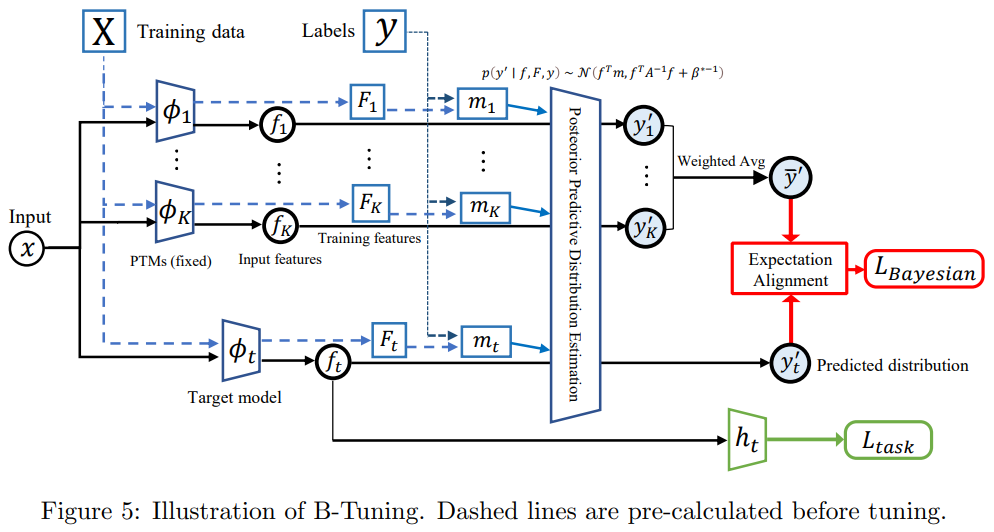
后验概率计算方式
首先给出如下结论,即给出「先验和似然」的形式,则可直接得到对应的「证据和后验」形式:
$$
\begin{aligned} &\text{已知}=\left\{ \begin{aligned} & [\text{先验}]\ \ p(\mathbf{x}) =\mathcal{N}\left(\mathbf{x} \mid \boldsymbol{\mu}, \mathbf{\Lambda}^{-1}\right) \\ & [\text{似然}]\ \ p(\mathbf{y} \mid \mathbf{x}) =\mathcal{N}\left(\mathbf{y} \mid \mathbf{A} \mathbf{x}+\mathbf{b}, \mathbf{L}^{-1}\right) \\ \end{aligned} \right.\\ &\text{求解}=\left\{ \begin{aligned} &[\text{证据}] \ \ p(\mathbf{y})= \mathcal{N}\left(\mathbf{y} \mid \mathbf{A} \boldsymbol{\mu}+\mathbf{b}, \mathbf{L}^{-1}+\mathbf{A} \mathbf{\Lambda}^{-1} \mathbf{A}^{\mathrm{T}}\right) \\ & [\text{后验}] \ \ p(\mathbf{x} \mid \mathbf{y})= \mathcal{N}\left(\mathbf{x} \mid \mathbf{\Sigma}\left\{\mathbf{A}^{\mathrm{T}} \mathbf{L}(\mathbf{y}-\mathbf{b})+\mathbf{\Lambda} \boldsymbol{\mu}\right\}, \mathbf{\Sigma}\right), \boldsymbol{\Sigma} =\left(\mathbf{\Lambda}+\mathbf{A}^{\mathrm{T}} \mathbf{L} \mathbf{A}\right)^{-1} \\ \end{aligned} \right. \end{aligned}
$$
上述结论的具体推导可参考【PRML 学习笔记】第二章 - 概率分布 (Probability Distributions) 中的 2.3.3 节。
言归正传,「我们的目标是求解 $p(y’\mid f,F,y)$」,如果我们将其看成「后验」,那就要给出先验 $p(y’\mid F,y)$ 和似然 $p(f\mid y’,F,y)$ 的形式,这显然非常困难。因此和之前 $\text{LogME}$ 思想一致,引入 $w$,将其看成「证据」,具体展开式如下:
$$
p\left(y^{\prime} \mid f, F, y\right)=\int_w p\left(y^{\prime} \mid w, f\right) p(w \mid F, y) \mathrm{d} w
$$
因此只要给出先验 $p(w\mid F,y)$ 和似然 $p(y’\mid w,f)$ 的形式,即可完成求解目标。首先根据 $\text{LogME}$ 中的假设,已知 $p\left(y^{\prime} \mid w, f\right) \sim \mathcal{N}\left(w^T f, \beta^{*-1}\right)$,因此现在的关键在于求解 $p(w\mid F,y)$。
继续应用上述结论,将 $p(w\mid F,y)$ 看成后验,则只需给出先验 $p(w\mid F,\alpha^{*})$ 和似然 $p(y\mid w,F)$ 的形式,即:
$$
\begin{gathered} p(w\mid F,\alpha^{*})=p(w\mid \alpha^{*})=\mathcal{N}(0,{\alpha^{*}}^{-1}I) \\ p(y\mid w,F)=\mathcal{N}(Fw,{\beta^{*}}^{-1}I) \end{gathered}
$$
因此可以得到 $p(w\mid F,y)$ 的形式:
$$
p(w\mid F,y)=\mathcal{N}(m,A^{-1})
$$
其中依据 $\text{LogME}$ 中定义,$A=\alpha^{*} I+\beta^{*} F^T F, m=\beta^{*} A^{-1} F^T y$。得到先验 $p(w\mid F,y)$ 和似然 $p(y'\mid w,f)$ 后,可以得到最终目标 $p(y'\mid f,F,y)$ 的形式:
$$
p(y'\mid f,F,y)=\mathcal{N}\left(f^T m, \beta^{*-1}+f^T A^{-1} f\right)
$$
Few-shot NAS
首先传统 NAS (Vanilla NAS) 为搜索算法搜出一个网络,就将其在训练集上从头训练,并将其在验证集上的精度作为评估指标。该方法可以很准确地评估网络好坏,但耗时非常长。
其次 One-shot NAS 则利用了一个过度参数化 (over-parameterization) 的权重共享超网络 (supernet),只需训练一遍这个超网络。随后搜索算法搜出的网络,可以直接继承 supernet 中的权重,无需再度训练,只需做一轮推断,就可以得到其在验证集上的精度。该方法效率很高,但准确度较低。
而本文提出的 Few-shot 介于上述两种方法之间,使得准确度与效率得到一定的平衡。其核心思想是对原始 supernet 中的复合边进行拆分,得到多个 sub-supernets,再对各 sub-supernets 依次进行训练。
以下图为例,(a) 展示了 One-shot NAS 的步骤,即首先定义一个 supernet,其中有大量复合边(即红绿操作均有)。将其训练完后,搜索算法给出 target 网络(其中不再有复合边),target 网络再从 supernet 中继承对应权重,在验证集上做一轮推断得到最终评估指标。
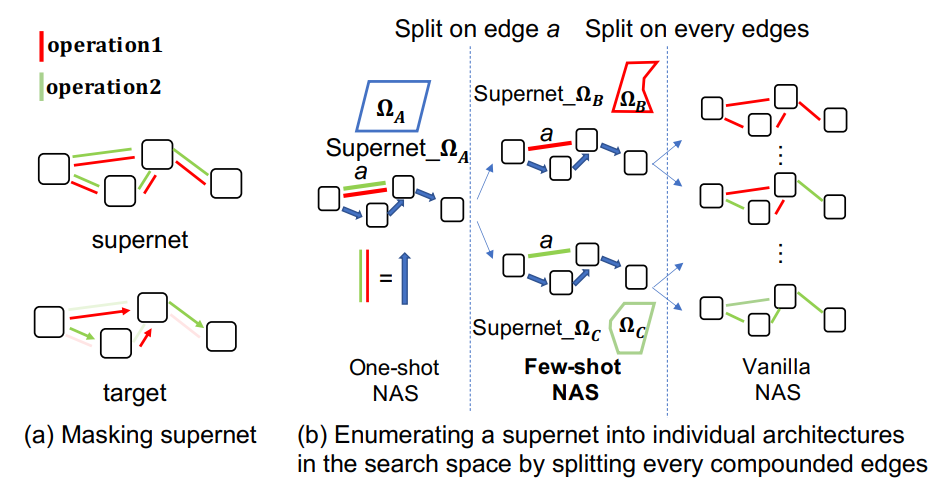
而 (b) 则展示了 Few-shot NAS 的步骤,即首先选中 supernet 中 a 这条复合边,对该边拆分后,得到两个 sub-supernets,而 sub-supernets 可以继续对复合边拆分,整个流程可以构建出如下的一棵树,而树中的叶节点 $\Omega_B,\Omega_C,\Omega_D$ 即为需要训练的 sub-supernets。
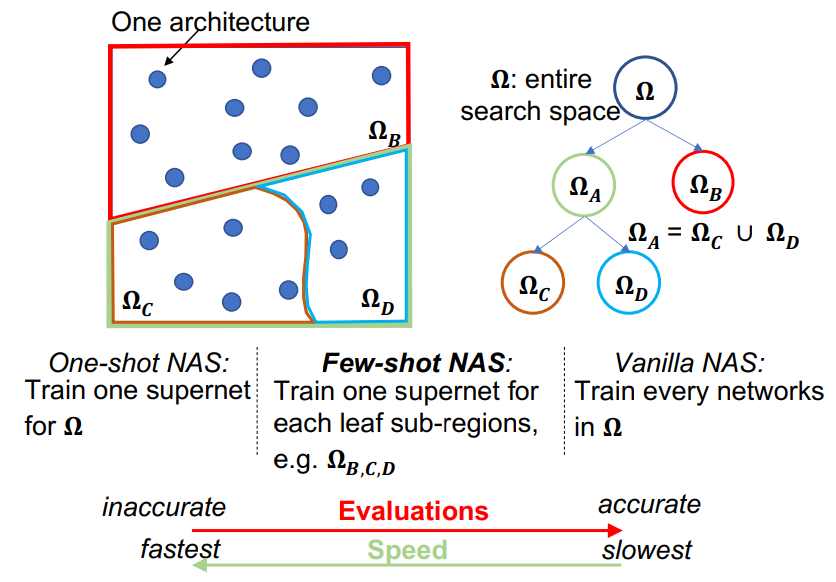
由此不难发现,Few-shot NAS 的实质就是对 One-shot NAS 中的 supernet 进行拆分,得到多个 sub-supernets,进而完成「效率下降」、「精度提升」的目的,具体实验结果如下所示:
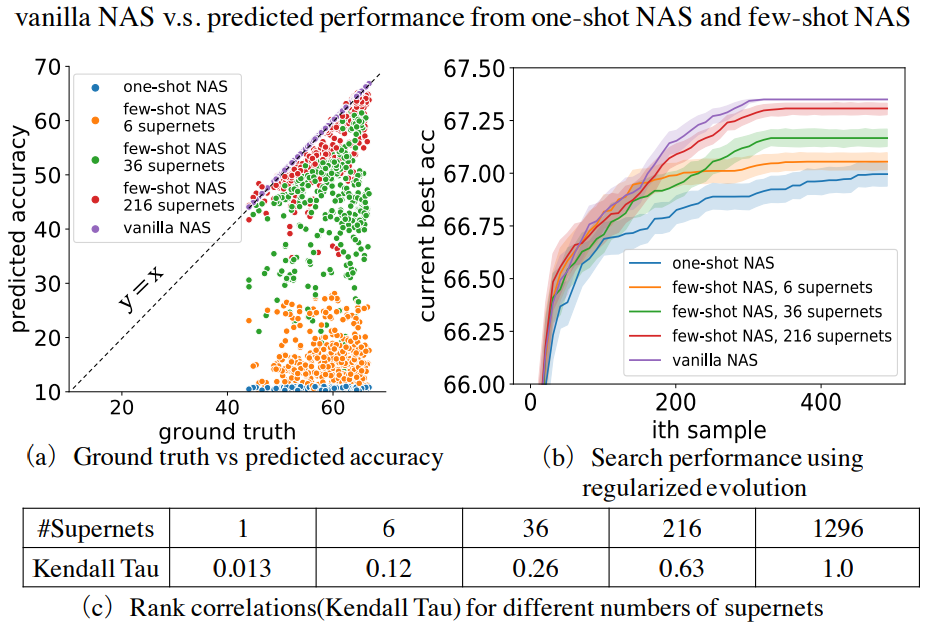
Zen-NAS
Neural Architecture Search (NAS) 系列工作旨在自动化搜索网络结构,降低从业人员设计网络的难度。
Zen-NAS 方法提出用 Zen-Score 来度量网络结构的好坏,而 Zen-Score 的计算仅与模型有关,无需训练数据。
该篇工作主要关注普通卷积神经网络(Vanilla Convolutional Neural Network, VCNN)的结构搜索,其主干仅包含卷积层、BN 层以及 RELU 激活层,其它成分均被移除(包括残差连接)。
Zen-Score 具体计算方式如下所示:
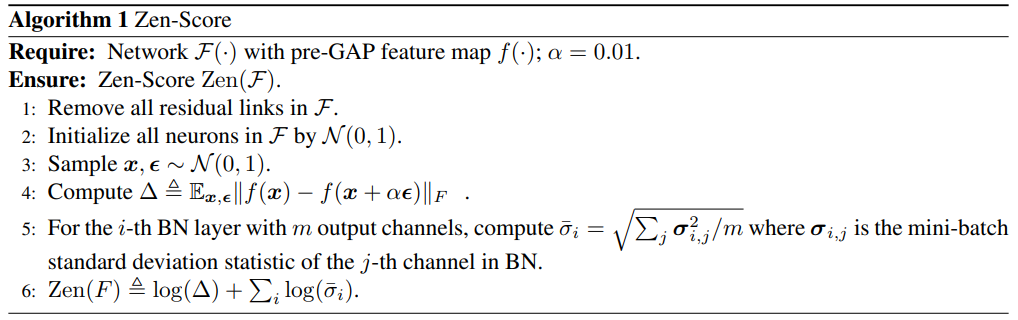
其数值主要与 $\Delta$ 和 $\boldsymbol{\sigma}_i$ 有关,前者可以认为是对模型梯度的度量,而后者则是对 BN 层方差的刻画。整体流程图如下所示:
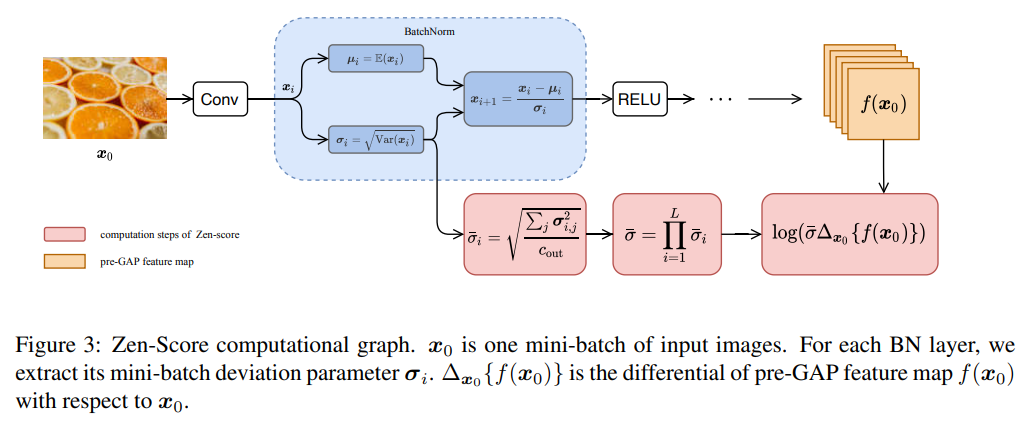
参考资料






