IJCAI23 - Continual Learning Tutorial

本篇 Tutorial 主要介绍了 CL 中的一些基本概念以及一些过往的方法。

Problem Definition

Continual Learning 和 Incremental learning 以及 Lifelong learning 属于同一概念，其所关心的场景均为「如何在新数据持续到来的情况下更新模型？」；并且由于存储空间和隐私问题，流式数据通常不能被存储。

CL 的整体目标为最小化所有已见任务的期望损失，如下所示：

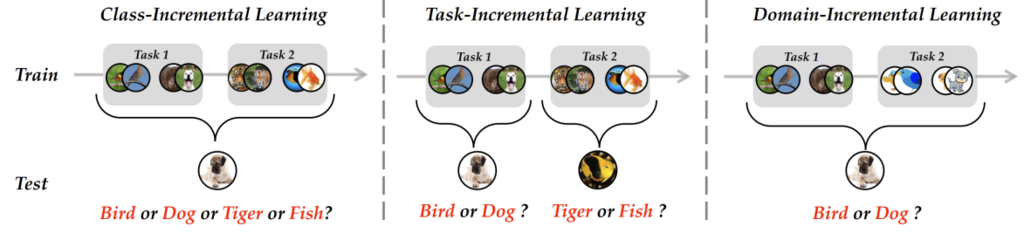
CL 又细分为三类（${\mathcal{Y}^t}$ 表示 $t$ 时刻的类别标签集合，$P(\mathcal{Y}^t)$ 表示类别分布，$P(\mathcal{X}^t)$ 表示输入数据分布）：

Class-Incremental Learning (CIL):

$$ \left\{\mathcal{Y}^t\right\} \subset\left\{\mathcal{Y}^{t+1}\right\},P\left(\mathcal{Y}^t\right) \neq P\left(\mathcal{Y}^{t+1}\right),P\left(\mathcal{X}^t\right) \neq P\left(\mathcal{X}^{t+1}\right) $$

Task-Incremental Learning (TIL): 测试时任务 $\text{id}(t)$ 已知

$$ \left\{\mathcal{Y}^t\right\} \neq\left\{\mathcal{Y}^{t+1}\right\},P\left(\mathcal{X}^t\right) \neq P\left(\mathcal{X}^{t+1}\right) $$

Domain-Incremental Learning (DIL):

$$ \left\{\mathcal{Y}^t\right\} =\left\{\mathcal{Y}^{t+1}\right\},P\left(\mathcal{Y}^t\right) =P\left(\mathcal{Y}^{t+1}\right),P\left(\mathcal{X}^t\right) \neq P\left(\mathcal{X}^{t+1}\right) $$

与其它相关领域的区别

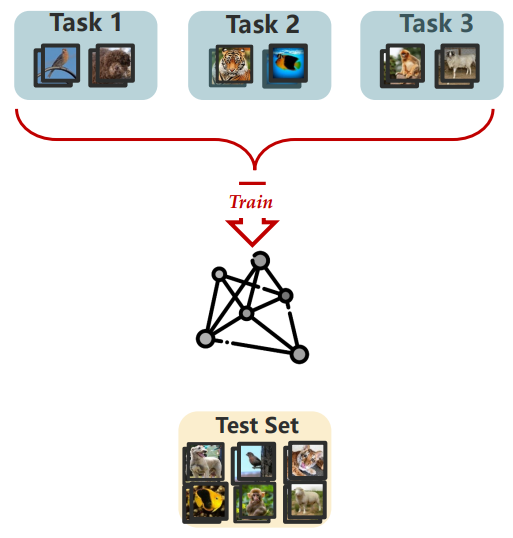
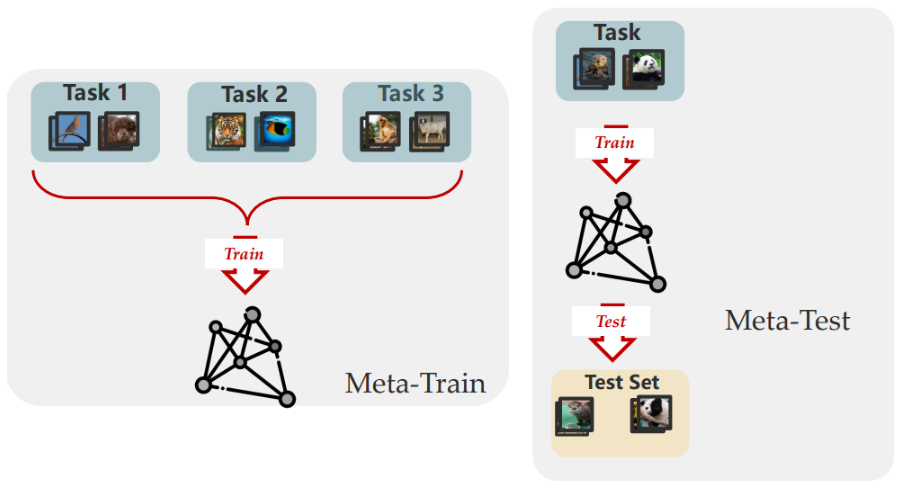
Multi-task Learning：（1）同时拿到所有任务的数据；（2）离线训练

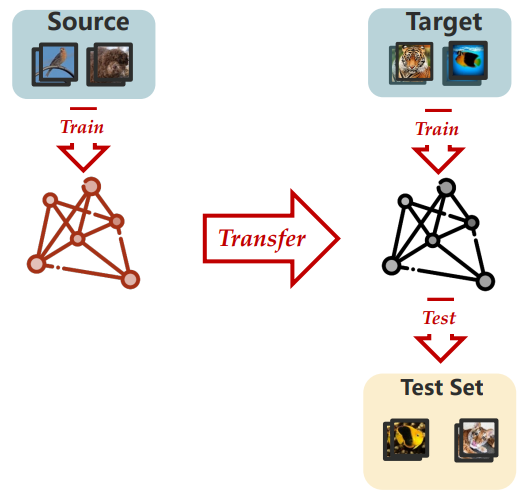
Transfer Learning：（1）只有两个阶段；（2）并且不关注第一阶段，即 Source 的性能

Meta-Learning：（1）离线训练；（2）不关心 meta-train 的性能

CL 的一些传统做法

具体方法分类如下：

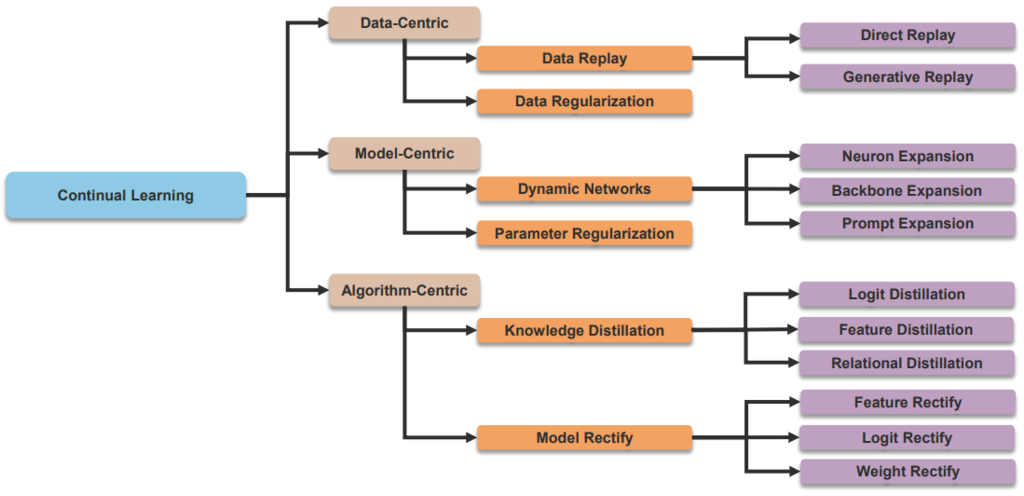
Data-Centric Methods

核心思想：保存一部分先前数据，在面对新任务时，可以作为训练损失的正则项 (hosting the data to replay former knowledge when learning new, or exert regularization terms with former data)

保存一部分数据的过往方法：

[Welling ICML’09] 计算 Embedding 空间的类中心，选取离类中心近的样本。
[Rebuffi et al. CVPR’17] 每个类依次贪心选取样本，使得样本 Embedding 均值逼近类中心。
[Shin et al. NIPS’17] [Gao and Liu ICML’23] 使用生成式模型学习每个类的数据分布。

将先前数据作为新任务训练损失正则项的一些方法：

[Lopez-Paz and Ranzato NIPS’17] 训练时要求模型不仅在新任务上做好，在旧任务上也要做的比之前好；模型在新任务和旧任务上的损失梯度夹角为正。

一些可能的问题：

[Verwimp et al. ICCV’21] Data replay 可能会遭遇 overfitting.
[Wu NeurIPS’18] 生成式模型也会出现灾难性遗忘。

Model-Centric Methods

核心思想：调整网络结构，或者识别网络中的重要参数并限制其变化

[Kirkpatrick et al. PNAS’17] 训练新任务时，限制模型参数的变化，越重要的参数权重越高

Algorithm-Centric Methods

核心思想：设计一些训练机制避免旧模型的遗忘 (design training mechanisms to prevent the forgetting of old model)

知识蒸馏 (Knowledge Distillation) 的相关方法：

[Li et al. TPAMI’17] 将旧模型作为 Teacher，训练时模型不仅要做好当前任务，在过去任务上需要表现得和 Teacher 尽可能相近。

模型纠正 (Model Rectify) 的相关方法：

例如「降低新类输出概率 Logit」和「降低最后一层新类的权重矩阵」。

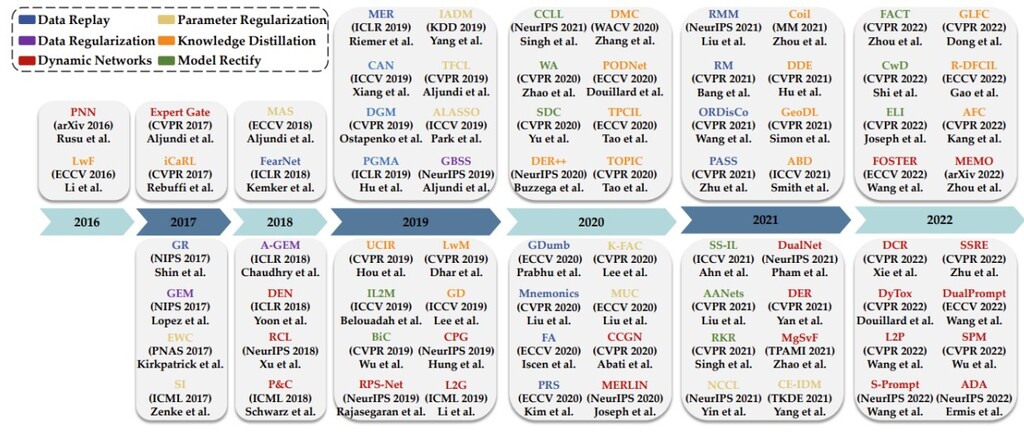
Trends of CL

最后是 CL 近几年的整体发展趋势：