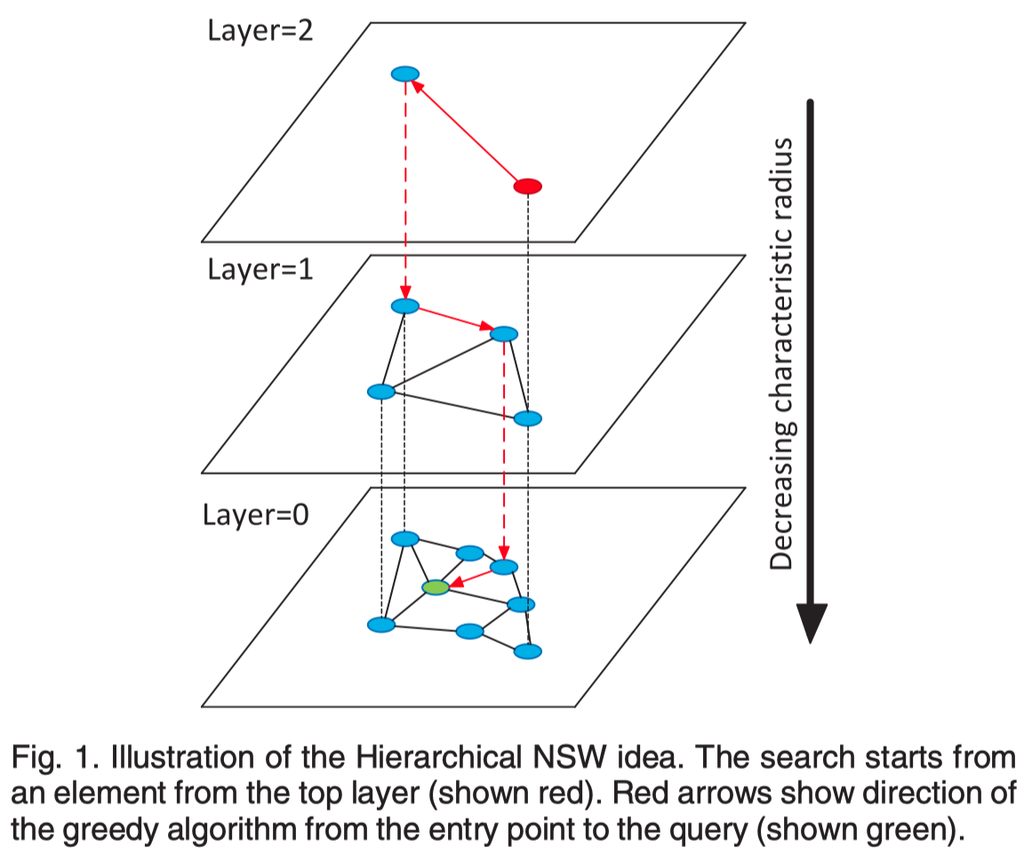
HNSW 算法的目标是从 $N$ 个数据点中,快速找到距离查询点最近的 $K$ 个数据点。其主要思想是构建一个层次图,其中每一层节点数自上而下递增,且每一层中的节点与其相近节点连边。基于这个层次图,查搜时可以贪心地自上而下搜索,每一层搜索时检查当前搜索节点的邻居是否更近,到达每一层的局部最优后,跳转至下一层,大致算法步骤如下图所示:
Delaunay Graph
HNSW 算法是对 NSW 算法的层次化扩展,而 NSW 算法的想法是构建近似 Delaunay 图的图结构,因此我们首先介绍一下 Delaunay Graph。
Delaunay 是满足特定条件的一种三角剖分(计算几何相关内容)。先介绍三角剖分,即对于给定的 $N$ 个点,输出一组三角形集合,其满足:
- 所有三角形顶点集合为初始的 $N$ 个点;
- 任意两个三角形的边除重合外,不相交;
- 所有三角形的并集构成初始 $N$ 个点的凸包。
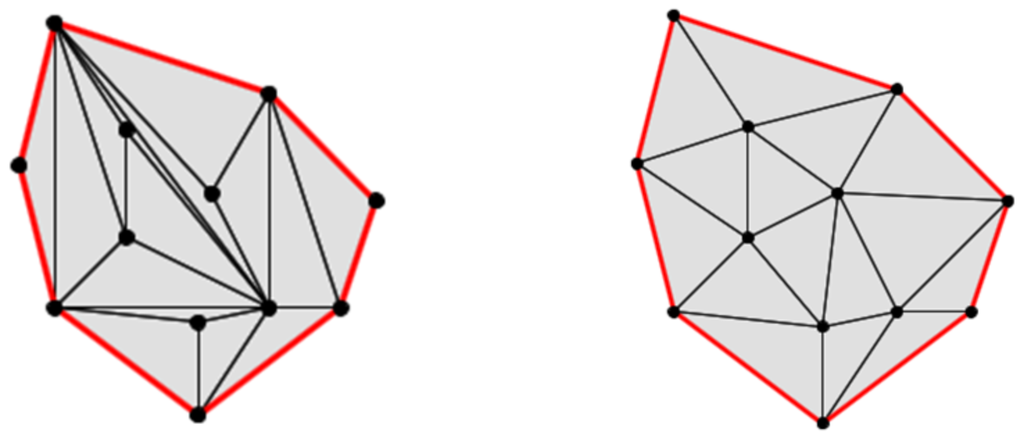
三角剖分不唯一,例如上述两幅图都满足三角剖分的性质。为找到一种结构更好且唯一的三角剖分,Delaunay 三角剖分增加了两个要求:
- 空圆性:任意三角形的外接圆范围内不会存在其它点;
- 最大化最小角:所有三角形中最小的角度最大(在所有可能的三角剖分中)。
满足上述三角剖分的 Delaunay Graph 由如下的一条性质:
- 采用基本的贪心策略可以找到距查询点最近的节点,而不会落入局部最优;
- 贪心策略:从任一点出发,迭代至距查询点最近的邻居点,要求邻居点距离比当前点距离更近,不断迭代直至收敛。
尽管 Delaunay Graph 性质较好,但对于高维数据来说,Delaunay Graph 的构建过于耗时,因此 NSW 算法的想法是构建近似 Delaunay Graph 的图结构。
Bowyer-Watson 算法
该算法是构建 Delaunay Graph 的一种常用算法(在二维平面上比较有效),此处顺带介绍一下。
算法一共分为三步,以下为大致的介绍:
- 平面上选取四个点构成一个长方形,使得初始 $N$ 个点都在这个长方形内部;此时连接长方形的一条对角线,即可构成一个包含两个直角三角形的初始三角剖分。
- 将初始 $N$ 个点逐一插入当前的三角剖分中,假设当前点为 $v$: i. 找到所有外接圆包含点 $v$ 的三角形,这些三角形的并集构成了一个区域; ii. 删除这些三角形的内部边,并将这个区域的边界顶点与 $v$ 相连,得到包含顶点 $v$ 的新三角剖分。
- 删除第一步中额外加入的最外围的 4 个点,并移除包含这些点的三角形,剩下的三角形即为最终的 Delaunay 三角剖分。
Hierarchical Navigable Small World (HNSW)
HNSW 搜索
由于 HNSW 的图构建算法需要用到图搜索算法,因此先对图搜索算法进行介绍。
如本文最开头所述,HNSW 采用自顶向下的搜索方式,在每一层中找到局部最优后,再进入下一层,其在每一层中的搜索算法如下所示:
- $ep$ 为搜索该层时选取的初始点(也可以包括多个点);
- $ef$ 为需要返回的近邻点数量;
- $W$ 为动态更新的近邻集合,其大小 $\leq ef$;
- 整体算法就是从初始点 $ep$ 出发,如果其邻居点比当前 $W$ 内的点更近,则更新 $W$,并从更近的点出发进行搜索,直到进入该层的局部最优。算法采用贪心的策略,可以主要关注候选点集 $C$ 的更新条件。

基于上述每一层的贪心搜索算法,可以得到最终完整的 $K$ 近邻搜索算法:
- 自顶向下搜索,每一层寻找唯一的最近点,并在下一层以当前最近点作为起始点;
- 此处的 $ef$ 表示最底层需要找的最近邻数量,最终的 $K$ 近邻在每一层得到的最近点集合 $W$ 中选取。

HNSW 图构建
HNSW 图构建采用的是逐步往图中添加新节点的方式,每个节点会先随机选取一个 Layer $l$,并同时出现在 $[0, l]$ 的所有层中。$l$ 越大,被选取的概率越低,呈指数衰减,具体如下所示: \begin{equation} l \leftarrow\left\lfloor-\ln (u n i f(0 . .1)) \cdot m_L\right\rfloor, \end{equation}
其中 $unif(0,1)$ 表示从 $[0,1]$ 中按均匀分布选取一个数值,$m_L$ 为超参数,通常设置为 $1/\ln(M)$,$M$ 为 HNSW 建图的超参数,表示每个新插入节点在每一层中连边的数量。
整体建图算法如下所示:
- $M_{max}$ 表示每个节点最多的邻居数;
- 新节点在每一层选邻居点时,先搜索 $efConstruction$ 个最近点(搜索的初始点由上一层的最近点决定),再从这些最近点中选择连边成为邻居的点,具体算法
SELECT-NEIGHBORS后文再介绍。

SELECT-NEIGHBORS 算法为上述建图算法中的关键子算法,原论文中提供了两种算法,第一种为在搜索得到的最近点集合 $W$ 中直接选取最近的 $M$ 个点连边,如下所示:

第二种采用了更加启发式的方法,即优先连接满足该性质的点:$e$ 距离新节点 $q$ 的距离比 $e$ 距离 $q$ 所有邻居的距离更近,则连接 $e$ 和 $q$。整体算法如下所示:
- $R$ 表示最终被选取连边的邻居集合;
- $extendCandidates$ 表示是否要扩展待选点集合,扩展的方式是将最近点的邻居也包含进来,默认值为 false;
- 由于该启发式方式连边条件比较苛刻,最终满足条件的点数可能达不到 $M$,此时若 $keepPrunedConnections$ 为 true,则可以在之前抛弃的点中选取最近点连接。

代码实现
HNSW 代码的具体实现可以调用现有开源包,例如 hnswlib、nmslib 以及 faiss,也可以参考 HNSW 算法简介,此处不再赘述。